La botella de Klein – La Ciencia de la Mula Francis

La definición más intuitiva de la botella de Klein (1882) se obtiene tomando un cuadrado, sea [0, 2π]×[0, 2π], e identificando las caras opuestas con una relación de equivalencia (u, 0) ∼ (u, 2π), y (0, v) ∼ (2π, 2π − v), como indican las flechas en la figura. Con cuidado se puede comprobar que resulta la «botella» que se interseca a sí misma que todos estamos acostumbrados.

Lo que mucha gente no sabe es que esta representación en forma de «botella» no es la única representación tridimensional de la botella de Klein. Otra representación muy famosa es la generada por el movimiento de una lemniscata en un círculo introducida en 1976 por T. Banchoff (cuya primera representación gráfica es de 1982 en un trabajo de S. Feiner, D. Salesin, and T. Banchoff).

Otra manera de visualizar la botella de Klein es mediante una familia uniparamétrica de círculos, siguiendo a H. B. Lawson en 1970.

Parecen representaciones de objetos diferentes, pero se pueden deformar entre sí demostrando que corresponden al mismo objeto.
El matemático y el aficionado a las matermáticas siempre se pregunta cómo se pueden describir matemáticamente las ecuaciones de estas representaciones. No es fácil. La famosa botella, en el software matemático Mathematica, está calculada mediante las fórmulas descritas en 1991 por S. Dickson (básicamente dos tubos adecuadamente conectados).

La expresión matemática de la botella de Lawon es un poco más sencilla,
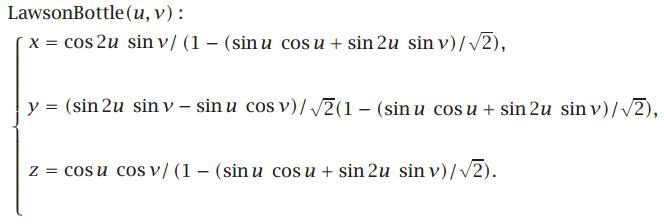
pero la más sencilla es la de Banchoff,

Aunque, obviamente, ninguna de estas expresiones matemáticas es fácil de entender. Gregorio Franzoni introduce una expresión matemática en su artículo «The Klein Bottle: Variations on a Theme,» Notices of the AMS 59: 1076-1082, 2012. M. Trott en uno de sus libros sobre Mathematica introdujo la idea de «engordar» en forma de tubo una curva y determinó las propiedades generales de la curva para garantizar que el resultado fuera una botella de Klein. G. Franzoni aplica dicha idea una curva piriforme, como ilustra esta figura.

La formulación matemática es muy sencilla. La curva es γ(t) y el radio en cada punto de dicha curva es r(t). La botella de Klein dibujada arriba corresponde a los parámetros indicados más abajo.

Aparentemente, más fácil imposible. Más información en Gregorio Franzoni, «The Klein Bottle: Variations on a Theme,» Notices AMS, Aug 2012.






