Statistical Process Control (SPC)
Statistical Process Control (SPC) is a statistical method to measure, monitor, and control a process. It is a scientific visual method to monitor, control, and improve the process by eliminating special cause variation in a process.
Mục lục
History of Statistical Process Control (SPC)
Though SPC effectively used in western industries since 1980, it was started during the twenties in America. Walter A Shewhart developed the control chart as well as the concept that a process could be in statistical control in 1924 at Bell Telephone Laboratories, USA. Likewise, the SPC concepts are included in the management philosophy by Dr. W.E. Deming just before World War II. However, SPC became famous after Japanese industries implement the concepts and compete with western industries.
Meaning of SPC
- Statistics: Statistics is a science that deals with the collection, summarization, analysis, and drawing of information from the data.
- Process: It converts input resources into the desired output (goods or services) with a combination of people, materials, methods, and machines as well as measurements.
- Control: System, policies, and procedures in place so the overall output meets the requirement.
Why use Statistical Process Control
Today companies are facing increasing competition and also operational costs, including raw materials continuously increasing. So for organizations, it is beneficial if they have control over their operation.
Organizations must make an effort for continuous improvement in quality, efficiency, and cost reduction. Many organizations still follow inspection after production for quality-related issues.
SPC helps companies to move towards prevention-based quality control instead of detection-based quality controls. By monitoring SPC graphs, organizations can easily predict the behavior of the process.
Statistical Process Control Benefits
- Reduce scrap and rework
- Increase productivity
- Improve overall quality
- Match process capability to product requirement
- Continuously monitor processes to maintain control
- Provide data to support decision making
- Streamline the process
- Increase in product reliability
- Opportunity for company-wide improvements
Statistical Process Control Objective
SPC focuses on optimizing continuous improvement by using statistical tools to analyze data, make inferences about process behavior, and then make appropriate decisions.
The basic assumption of SPC is that all processes are generally subject to variation. To that end, Variation measures how data are spread around the central tendency. Moreover, variation may be classified as one of two types, random or chance cause variation and assignable cause variation.
Common Cause: A cause of variation in the process is due to chance but not assignable to any factor. It is the variation that is inherent in the process. Likewise, a process under the influence of a common cause will always be stable and predictable.
Assignable Cause: It is also known as “special cause”. The variation in a process that is not due to chance therefore can be identified and eliminated. In this case, a process under influence of a special cause will not be stable and predictable.
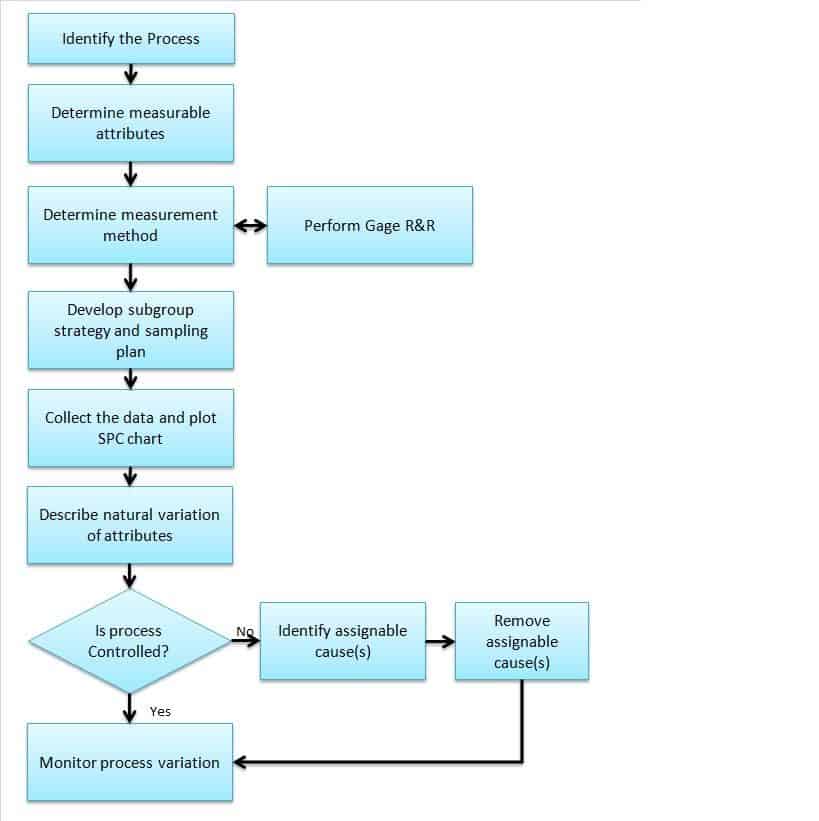
How to Perform SPC
1. Identify the processes:
Firstly, identify the key process that impacts the output of the product or the process that is very critical to the customer. For example, plate thickness impacts the product’s performance in a manufacturing company, then consider the plate manufacturing process.
2. Determine measurable attributes of the process:
Secondly, identify the attributes that need to be measured during production. For example, consider the plate thickness as a measurable attribute.
3. Determine the measurement method and also perform Gage R&R:
Thirdly, create a measurement method work instructions or procedure including the measuring instrument. For example, consider thickness gauge to measure the thickness and create an appropriate measuring procedure. Perform Gage Repeatability and Reproducibility (Gage R & R) to define the amount of variation in the measurement data due to the measurement system.
4. Develop a subgroup strategy and sampling plan:
Fourthly, determine the subgroup size based on the product’s criticality and determine the sampling size and frequency. For example, collect 20 sets of plate thicknesses in a time sequence with a subgroup size of 4.
5. Collect the data and plot the SPC chart:
Then, collect the data as per sample size and select an appropriate SPC chart based on data type (Continuous or Discrete) and also subgroup size. For Example, for plate thicknesses with a subgroup size of 4, select Xbar -R chart.
6. Describe the natural variation of attributes:
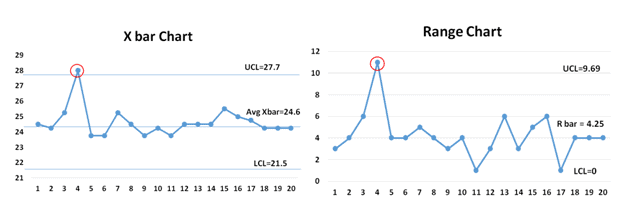
Next, calculate the control limits. From the above example, calculate the upper control limit (UCL) and lower control limit (LCL) for both Xbar Ranges.
7. Monitor process variation:
Finally, interpret the control chart and check whether any point is out of control and the pattern. Example: check the Xbar R chart if the process is not in control, then identify the assignable cause(s) and address the issue. This is an ongoing process, so monitor the process variation.
Additional Statistical Process Control Resources
Control limits are the voice of the process (different from specification limits, which are the customer’s voice.) They show what the process is doing and act as a guide for what it should be doing. Control limits also indicate that a process event or measurement is likely to fall within that limit.
Control charts: A Control chart is one of the primary techniques of statistical process control (SPC). The control chart is a graphical display of quality characteristics that are measured or computed from a sample versus the sample number or time. Furthermore, the control chart contains a center line that represents the average value of the quality characteristics and two other horizontal lines known as the upper control limit (UCL) and lower control limit (LCL)
Selection of an appropriate control chart is very important in control chart mapping. Otherwise, it ended up with inaccurate control limits for the data. The selection of the control chart depends on the data type: Continuous or Discrete?
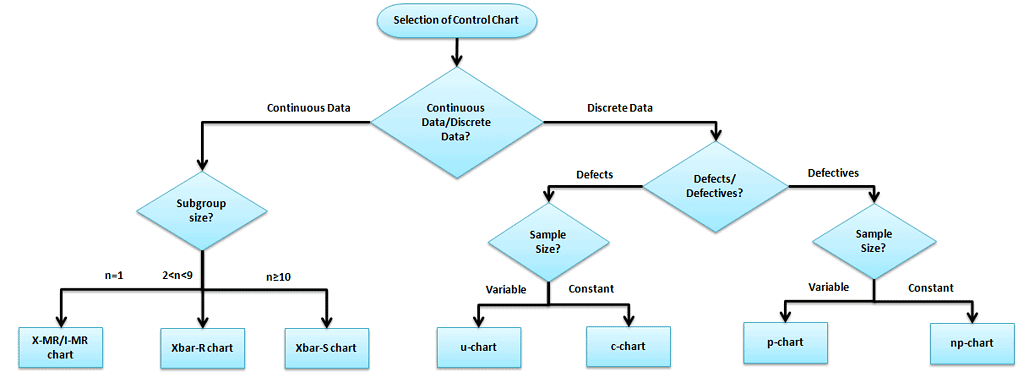
Variable (Continuous) Control Charts
Measure the output on a continuous scale. It is possible to measure the quality characteristics of a product.
X bar – R Charts (when data is readily available)
- X bar R chart is used to monitor the process performance of continuous data and the data to be collected in subgroups at set periods. In other words, it is two plots that monitor the process mean and the process variation over time
- A run chart displays observed data as they evolve over time. Just a basic graph that displays data values in a time order. Can be useful for identifying trends or shifts in the process but also allows you to test for randomness in the process.
X – MR Charts (I – MR, individual moving range)
- An I-MR chart is also known as an X-MR chart. An Individual moving range (I-MR ) chart is used when data is continuous and not collected in subgroups. In other words, collect a single observation at a time. An I-MR chart provides process variation over time in a graphical method.
X bar – S Charts (when sigma is readily available)
- X Bar S charts often used control charts to examine the process mean and standard deviation over time. These charts are used when the subgroups have large sample sizes, and the S chart provides a better understanding of the spread of subgroup data than the range.
- The EWMA – Exponentially Weighted Moving Average chart is used in statistical process control to monitor variables (or attributes that act like variables), and additionally, it makes use of the entire history of a given output. This is different from other control charts that tend to treat each data point individually.
The output is a decision or counting. It is not possible to measure the quality characteristics of a product. In other words, it is based on the visual inspection like good or bad, fail or pass, accept or reject.
- p Charts: (for defectives – sample size varies) – Use P chart when the data are the fraction defective of some set of the process output. It may also be shown as a percentage of defective. The points plotted on the p-chart are the fraction of non-confirming units or defective pieces found in n samples.
- np Charts (for defectives – sample size fixed) – Use an np-chart when the data is collected in subgroups that are the same size. np-charts show how the process, measured by the number of nonconforming items (defectives) it produces, changes over time. In other words, the process describes pass or fail, yes or no.
- c Charts (for defects – sample size fixed) – Use c charts when the data are concerned with the number of defects in a product. The number of defects collected for the area of opportunity in each subgroup.
- u Charts (for defects – sample size varies) – A u chart is an attribute control chart that displays how the frequency of defects, or nonconformities, is changing over time for a process or system. The number of defects collected for the area of opportunity in each subgroup.
Great decision matrix here: https://www.moresteam.com/toolbox/statistical-process-control-spc.cfm
Statistical Process Control Videos
Six Sigma Green Belt Statistical Process Control Questions
Question: In the Control Phase of a LSS project a Belt will identify key metrics that can be monitored and analyzed to give an indication that a process may be moving towards an out of spec condition. When he applies this approach he is using __________________.
(A) Poisson Derivatives
(B) Inferential Statistics
(C) Kanban Analysis
(D) Statistical Process Control
Answer:
Unlock Additional Members-only Content!
To unlock additional content, please upgrade now to a full membership.
Upgrade to a Full Membership
If you are a member,
To unlock additional content, please upgrade now to a full membership.If you are a member, you can log in here.
Question: Statistical process control (SPC) is best defined as the use of
(A) Pareto charts to understand and control a process
(B) inputs to control critical and complex processes
(C) statistical methods to identify and remove manufacturing errors
(D) statistical methods to understand and control a process
Answer:
Unlock Additional Members-only Content!
To unlock additional content, please upgrade now to a full membership.
Upgrade to a Full Membership
If you are a member,
To unlock additional content, please upgrade now to a full membership.If you are a member, you can log in here.






