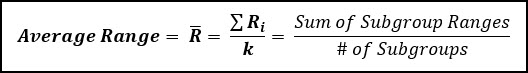Statistical Process Control (SPC)

What gets measured gets managed – Peter Drucker

This is incredible relevant to the topic at hand – Statistical Process Control (SPC).

Your success if a direct reflection of your process.

If you’re not managing your processes you’re not going to like the result you get.

SPC, and more specifically the control chart, is one of the best tools out there to help you manage and control your process.  So, what is SPC?

Statistical Process Control (SPC) is a collection of tools that allow a Quality Engineer to ensure that their process is in control, using statistics 😊.

The most common SPC tool is the control chart which is our focus of this chapter.

This chapter starts the objectives and benefits of SPC & Control Charts.

Then we explain the “WHY” behind SPC, which is variation, and the two types of variation that all processes experience.

Next, we review the process of creating a control chart, which starts with selecting the right variable to monitor, and the concept of rationale subgroups.

Then we review 3 common variable control charts and 4 attribute charts.

For variable charts, I’ll explain the I-MR, the X-bar & R, and the X-bar and S chart.
For attribute charts, I’ll explain the p-chart, np-chart, c-chart and u-chart.

Once we’ve identify and constructed our control chart, it’s time to analyze our control chart. We will review the various rules you should be using to determine if you’re in statistical control.

This is the bulk of SPC, but before we close out we will wrap up with two other topics, Pre-control charts, and short run SPC. We’ll give a brief intro into these tools and how the work.

Ok, let’s get with the objectives and benefits of SPC and control charts.

Objectives & Benefits of SPC and Control Charts

SPC was born in the 1920’s when Walter Shewhart developed the first control charts. Since then, many other quality gurus have expanded on these early control charts to give us what we have today.

In general, SPC is a collection of tools and techniques used to measure and analyze process data in order to characterize the behavior of our process and achieve process control.

The most common SPC tool is the control chart, which will be the focus of this chapter.

In simple terms, a control chart tool is a mirror that reflects the performance & behavior of your process. A control chart can also be described as a visual communication tool that graphs analyzed data in real-time.

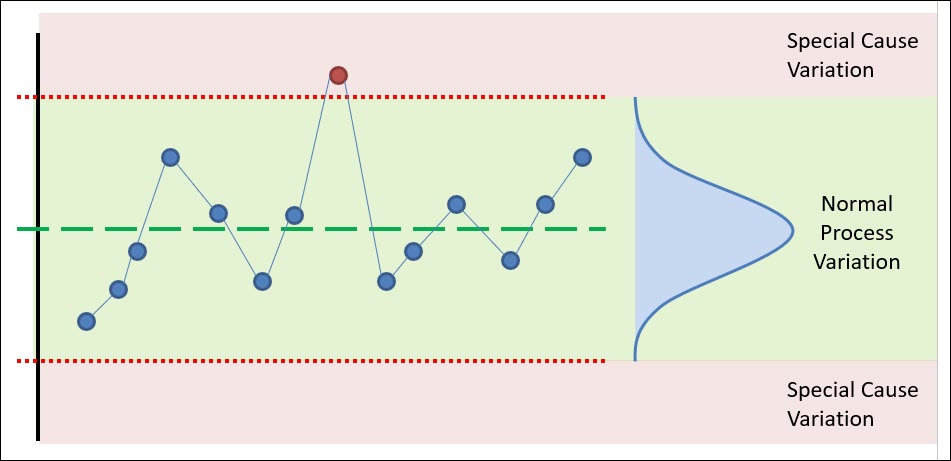
Having a visual tool that reflects real-time data that represents the health of a process allows you to proactively monitor and control your process – making adjustments or corrections when they’re needed.  This Is the primary objective of a control chart.

Using control charts results in a number of possible benefits depending on your process and situation. Below I’m going to start with the secondary benefits because the primary benefit will naturally transition us into the next section on variation.

Secondary Benefits of Control Charts

One important secondary benefit of a control chart is the ability to measure the impact of improvement efforts. Within the DMAIC process is step 2, Measure, and step 5, Control. A control chart can be used in either steps of this process.

Another benefit of collecting data about your process over time is that it naturally facilitates the ability to measure the capability of your process.

Lastly, SPC can also be used in certain instances to begin to predict when problems will occur and prevent them.

For example, tool wear can cause a drift in a part dimension, which can be detected prior to it resulting in non-conforming material.

Primary Benefits of Control Charts

Ok, so let’s jump into the primary benefit of a control chart.

As you know, a control chart is used to reflect the performance of a process, and the performance of a process can be described by the average value of the process, and the variation associated with the process.

This is important – every process has natural variation that’s common to the process. This variation is caused by the natural and normal variation in the environment, the equipment, the facility, the people, etc.

There’s a second kind of variation that not natural to your process and this second kind of variation is not your friend!

This variation is often called special cause variation because it’s not common or natural to your process and can be attributed to a specific cause or problem (that should be eliminated 😊).

When this type of variation is present – problems occur.

The primary benefit of a control chart is its unique ability to separate the normal variation within your process and the special cause variation.

Being able to distinguish between these two types of variability allows you to take action on your process only when necessary.   Let’s jump into these two types of variation.

The Two Types of Variation within a Process

Let’s use an example to demonstrate these two types of variation.

Common Cause Variation

You’ve sampled from your process and found that it produces product that follows the normal distribution – by the way, this is a very important assumption for the use of a control chart – that your process follows the normal distribution.

When a process is stable, it only experiences variation that is common, normal and inherent in the process. These common causes of variation cannot be eliminated without significantly redesigning the process.

When a process is not experiencing any special cause variation, you’d expect to find this same distribution tomorrow, next week, next month and next year.

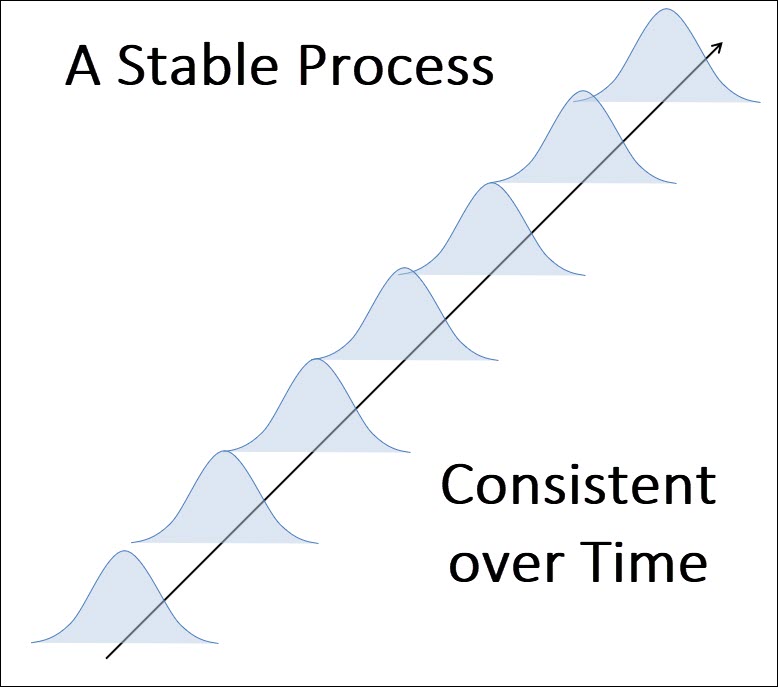
This is the ideal state for your process – this is the goal of SPC – to result in a consistent, predictable process over time.

You want to get the same results day after day, and a control chart can help get you there.

Now, your stable process might have more variation that you’d want – and the only way to change that is to make a major change to your process to reduce the variation – this is the essence of six sigma.

Oftentimes this normal process variation can result in problems, however the second type of variation, special cause variation is even more sinister.

When something goes wrong, it’s important to know if the issue is due to common cause variation or the second type of variation, special cause variation.

Special Cause Variation

Special cause variation is any type of variation that can be attributed to a special cause or situation that’s influencing your process.  These special causes impact your process in negative ways and result in instability and unpredictability.

Perhaps one of your raw material vendors has sent you non-conforming material – this is special cause variation.

Perhaps a piece of equipment has blown a gasket and is acting up – this is special cause variation.

Special causes should be identified quickly and removed as they result in an unstable process over time:

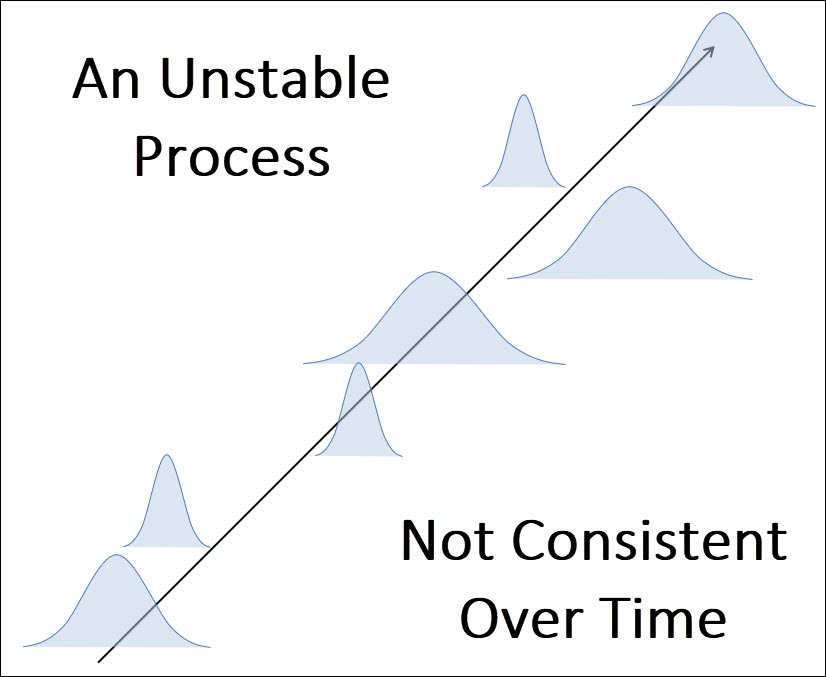
The primary benefit and purpose of a control is to help you identify when your process is being influenced by special causes of variation.

Being aware of this variation allows you to work through your CAPA process to identify the root causes of that variation and eliminate it – which is the true benefit of a control chart.

Being able to distinguish between common and special cause variation will also prevent you from over-reacting to common cause variation.

So how do we distinguish between normal variation and special cause variation – we use a control chart!

Let’s review the elements of a control chart so that you can see how a control chart distinguishes between common cause variation and special cause variation.

The Three Key Elements of a Control Chart

Below is a basic control chart, with its 3 key elements, the Center Line, the Upper Control Limit and the Lower Control Limit.

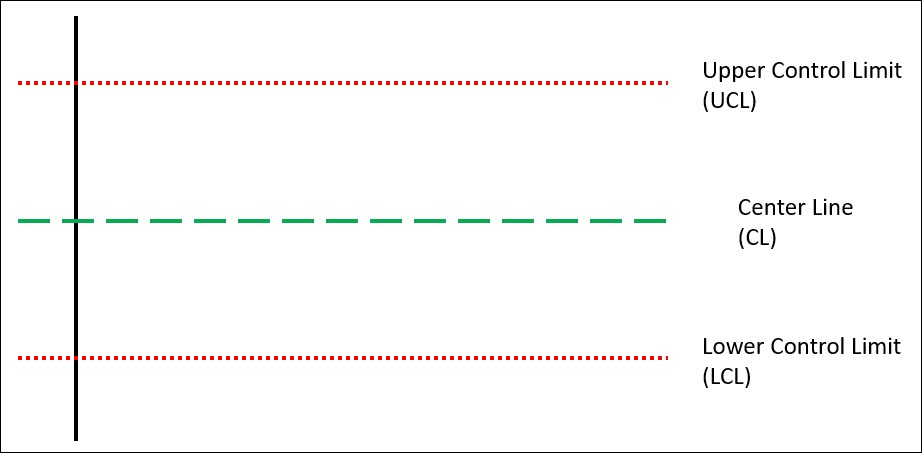
Whether you’re using attribute or variable data, all control charts will contain these 3 elements.

These 3 elements allow the control chart to distinguish between common cause variation and special cause variation.

The truly special elements of the control charts are the control limits, and these limits create the boundaries between common cause variation and special cause variation.

Typically, these control limits are set at +/- 3 standard deviations away from the average value (center of the process). Thus, if your process is stable (not changing over time), then 99.73% of your population should fall within the control limits.

It is very important to note that these elements of the control chart (Centerline & Control Limits) are not associated with your specification limits or customer requirements.

These control limits and centerline represent the “voice of the process” and are simply a reflection of the process – both the average value of your process and the natural variation of the process.

These control limits do not reflect the “voice of the customer” – meaning that they have nothing to do with your specification limits.

Below we will review different types of control charts and they all have these key elements that allow you to distinguish between common and special cause variation.

There are a handful of other “rules” that we will go over later in the chapter, but first we must discuss how to create a control chart.

Selection of Variables

When creating a control chart, the first factor you must consider is which variable within your process will be controlled, and what type of data is available for that process variable.

Regarding the type of data – we will review the difference between continuous and discrete data below as this will determine the type of control chart you should use.

Then we will go into a special discussion about discrete data and the key difference between a defect and a defective.  This is an important concept in control charts that you must be familiar with.

Lastly, I’ll integrate the pareto principle into this process of selecting the proper variable to use with a control chart.

Continuous v. Discrete data

Ok, so I’ve stolen all of this from a previous chapter on collecting and summarizing data, if you need a refresher, go check that out.

Discrete data is any data that is limited to a specific range of data and cannot be more precise.  Discrete data usually involves whole integers (1, 2, 3, 4); or can often simply be pass/fail or good/bad assessments.

Discrete data includes things like the number of defects per lot, Pass/Fail data, True/False data, the count conforming/non-conforming product, the number of defectives per Lot, etc.

You may also see discrete data called attribute data or counted data.

Continuous Data is any data set that can be measured across a wide scale and can be reduced to finer & finer results.  The height of the table is 38.2840 inches.   The TV has been on for the last 1,458.79 seconds.

So continuous data can take any value on the real number line while discrete data can only take on limited values.

Hopefully at this point in your CQE journey, you’re familiar enough with discrete and continuous data to know the difference.

If you’re using discrete data, you’re going to have to determine if you’re measuring defects of defectives.

Let’s discuss this now.

Defect v. Defective

A defect and a defective are not the same thing – not by a long shot.

A “defective” is an entire unit that fails to meet specifications.  A “defect” is an undesirable condition within a unit.

If a unit has a defect on it, it is defective, however a single defective unit can have multiple defects associated with it.

Below is a car door that’s been inspected for defects – scratches, paint runs, paint bubbles.

This single car door is a “defective unit” that could be trended, or each individual defect (scratches, paint runs, paint bubbles) can be trended.

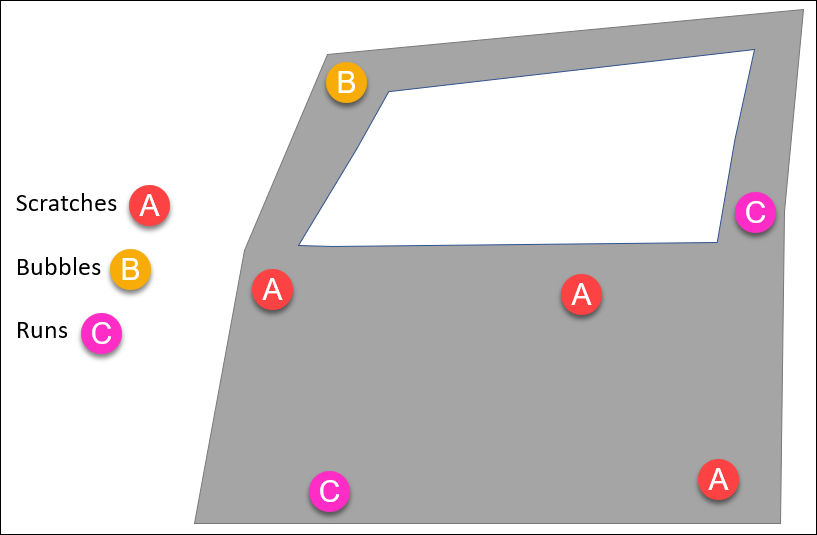
As a Quality Engineer setting up a control chart you can choose to simply trend the number defectives (car doors which do not pass inspection), or you can get specific and choose to monitor the occurrence of specific defects (runs, bubbles, etc).

Be careful if you use defects to be crystal clear about which defects you’re trending for. If you’re not clear, and you add more defects over time, it will create a false signal.

Using the Pareto Principle to Select a Variable to Control

Control charts are awesome, and they’ve got a ton of benefits. So, you might be tempted to create a control chart for every quality characteristic or process variable available.

However, using the pareto principle is a wise thing to do when selecting a variable to control chart. That is, there are a critical few process parameters (Key Process Inputs or Key Process Outputs) that reflect the health of our process.

There are a few factors to consider when determining the critical few parameters to control chart:

• the correlation between that variable and the process, (is it a key process variable)
• the criticality of the variable in terms of risk to the customer or product functionality,
• the potential financial benefits or consequences associated with a variable,
• the difficulty associated with implementing and maintain a control chart.

Another common recommendation is to pick a variable that is upstream in your process so that you detect the special cause variation early.

The Process Design phase is the perfect time to identify these key process variables that should be control charted.

What Is Rational Subgrouping

The last critical concept when setting up your control chart is the idea of a Rational Subgroup.

With control charts, we’re taking samples from your process, measuring those samples and then making a conclusion as to whether the process is in control or not.

The control limits on your control chart are based on the variability within those samples taken.

Thus, the way you take samples has a huge impact on the overall sensitivity of your control chart.

This is why we must determine a “rational subgroup” of samples to take.

A rational subgroup is defined as a collection of units that are all produced under the same conditions.

These samples should be as homogenous as possible, and any variation within these samples should only include the normal, inherent process variation.

This rational subgroup is usually a snapshot of your process at any moment in time.

By only including the normal process variation in our rational subgroup, we ensure that the control limits on our control chart are appropriately sensitive to special causes of variation.  

I’ll say that again for effect.

The variation within your subgroup of samples is what determines the control limits for the process, and we want to minimize this within-group variation so that our control chart will be sensitive to any special causes of variation over time.  

Below is an example of a rational subgroup where 5 samples are taken in the subgroup, and you can see how the “within subgroup” variation is defined.

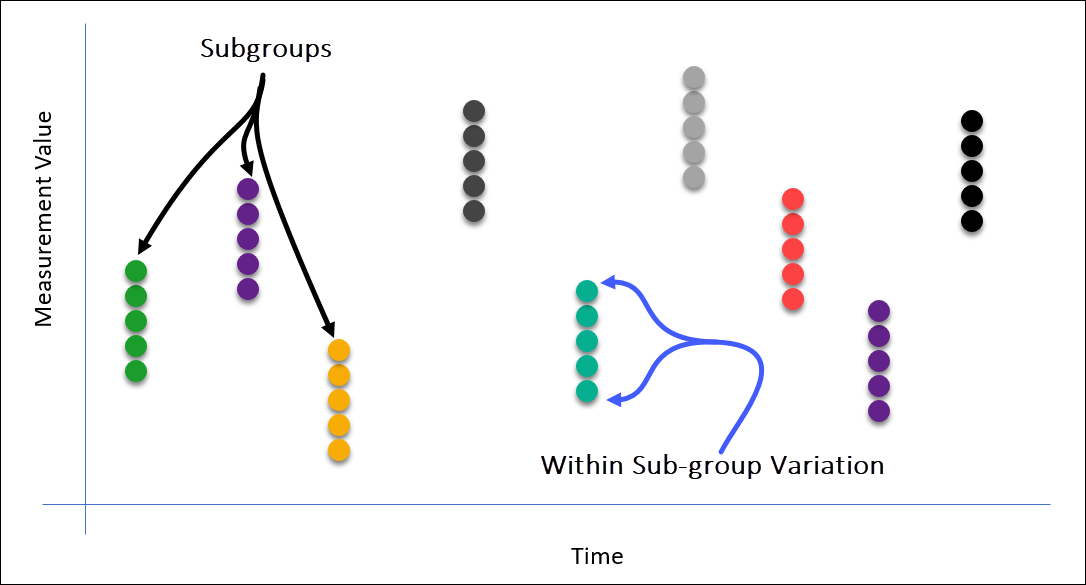
With an X-bar R chart, this is the range within the subgroup (R-bar) which is used to calculate the control limits of the chart.

Remember, you want to choose a rational subgroup that minimizes the variation within that subgroup which maximizes the opportunity for variation between subgroups.

This way, if there is a process change, the control chart will detect it.

Not having a properly defined rational subgroup can hide process changes or indicate process changes where in actuality none exist.  Rendering your control chart useless.

Types of Control Charts

Alright, time to jump into the meat of the chapter!

Let’s start with control charts for variable data, then move on to control charts for attribute data.

We cover the 3 most common control charts for variable data – X-bar & R Chart, the X-Bar & S chart and the I-MR chart.

Then, we will review the 4 most common control charts for attribute data – the p-chart, np-chart, c-chart and u-chart.

Besides being two different types of data, these two groups of control charts also have another key different.

Variable control charts always work in pairs while attribute charts are a single chart.

For example, an X-bar and R chart is two charts – an X-bar chart monitors the average value of the process and a Range (R) chart that monitors the variation of the process.

However, a c-chart is simple a single chart that monitors defects over time.

There are pros and cons to both types of charts, and as a Quality Engineer you’ll have to weigh these against each other to pick the right chart.

In general, variable data control charts tend to be more sensitive to process changes (😊) but can also be more expensive and difficult to administer (more math ☹).

Variable Control Charts

The 3 Most Common Variable Control Charts

Let’s start with variable control charts, which include the X-bar & R Chart, the X-Bar & S chart and the I-MR chart.

Like I said above, Variable control charts always work in pairs, with the first chart monitoring the process average, and the second chart monitoring the process variability.

For example, the X-bar chart monitors the central tendency of your process. The Individuals (I) Chart is also a representation of the central tendency of your process.

Similarly, the R (Range) Chart, S (Standard Deviation) Chart and the MR (Moving Range) Chart all reflect the variability in your process.

How to Choose the Right Variable Control Chart

When deciding which control chart to use, the one factor to consider is the sample size of the rational sub-group.

If you’re rational sub-group size is a single value (1), then you’ll use the I-MR (Individual and Moving Range) Chart.

If you’re rational sub-group size is between 2 – 10, then you’ll use the X-Bar and R Chart. When the sample size is less than 10, the Range of the sample data is a better estimator of the process variability than the standard deviation.

If you’re rational sub-group size is greater than 10, then you’ll use the X-Bar and S Chart.  When you’ve got 10 or more samples in a rational sub-group, then the best estimator of the process variability is the standard deviation.

Ok, let’s jump into the X-bar and R Chart to see how to construct and analyze this chart.

X-bar & R Charts

the X-bar and R chart is the workhorse of control charts. It is the most common control chart for variable data.

This control chart should be used anytime your rational subgroup size (n) is between 2 & 9, (2 < n < 9).

Like other variable control charts, it works in a pair.

The first chart is the X-bar chart, which monitors the subgroup mean of your process.

The second chart is the R chart, where R stands for Range.

As you know, the Range of a data set is one way to estimate the variability or spread associated with a process.  So, the Range chart monitors the variability of the process.

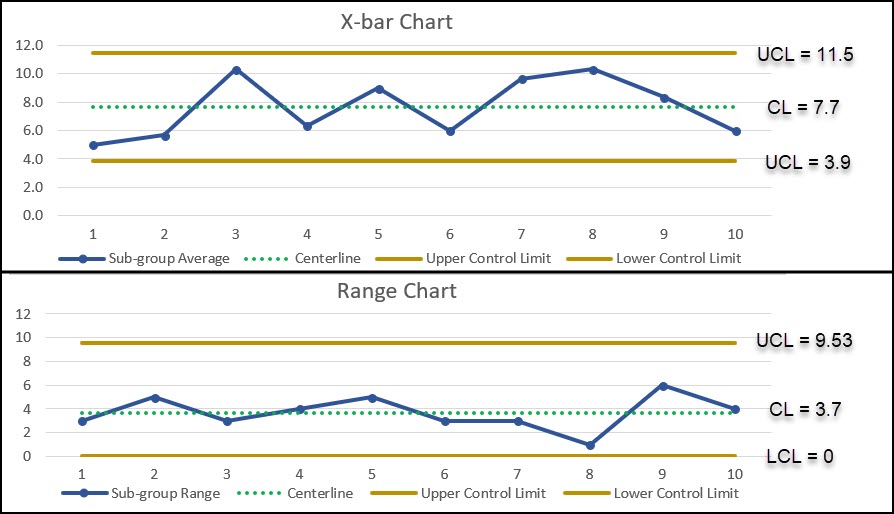
Below is an example of a X-bar and R Chart where our sub-group size is 3.

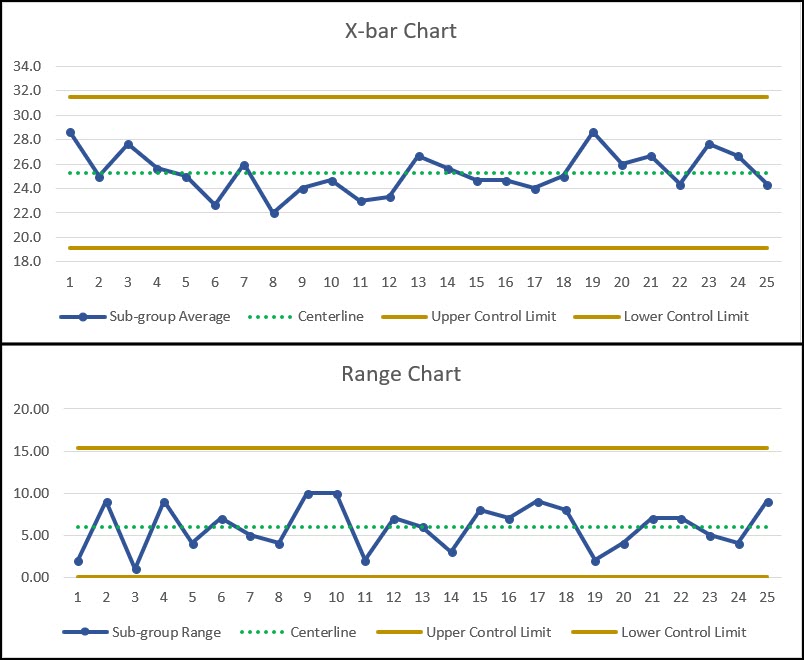
As you can see, both charts have the three elements discussed above, the CL (Centerline), the UCL (Upper Control Limit) and the LCL (Lower Control Limit).

X-Bar Chart Critical Elements

Below are the calculations for those critical elements on the X-bar chart:

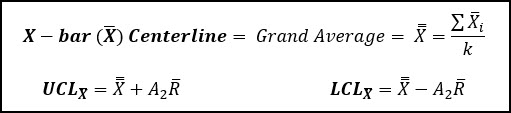
The centerline of the X-bar chart, is also called the grand average, and is also called X-double bar. This is the average of the averages, and it is the best estimate of the population mean (μ) for your process.

The UCL and LCL are calculated using the grand average, the average range (R-bar), and a factor (A2), which varies depending on the size of your subgroup.

The A2 factor is below, and in this instance with a sub-group size of 3, A2 is equal to 1.023.

Range (R) Chart Critical Elements

Moving on to the Range Chart, below are the calculations for the centerline, UCL & LCL for the range chart.

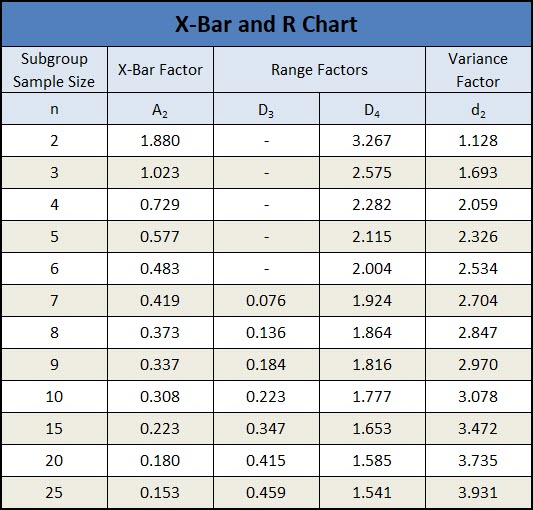
To calculate the control limits for the range chart, we multiply the average range (R-bar) by two factors (D4 & D3), which are based on the subgroup size (n) and can be found on the table below.

Just like the grand average is a good estimate of the population mean (μ), you can use your R-bar value to calculate an unbiases estimate of the population standard deviation using a constant (d2).

X-Bar and R Chart Constants

Below are the constants that must be used to calculate the critical elements (CL, UCL, LCL) of the X-bar and R chart.

X-Bar and R Chart Example

Let’s use the following data to calculate the centerline, UCL and LCL for an X-bar and R Chart.

Normally, you’d want to use at least 25 sub-groups from a stable process to calculate your control limits, but this limited data set of 10 sub-groups makes the math a little easier.

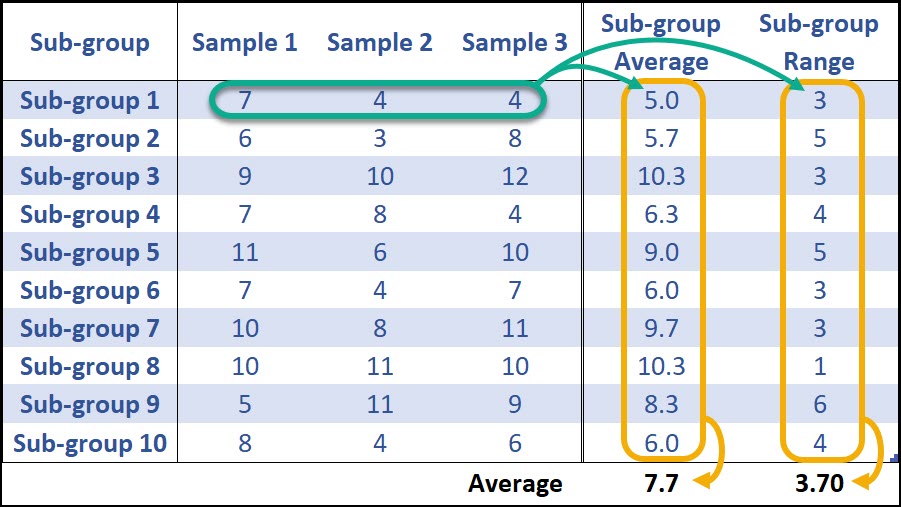
First, the 3 samples from each of the sub-groups (k = 10) are averaged to calculate the sub-group average. Then all of the sub-group averages are averages to calculate the grand average (7.7).  Same for the Range of each sub-group.

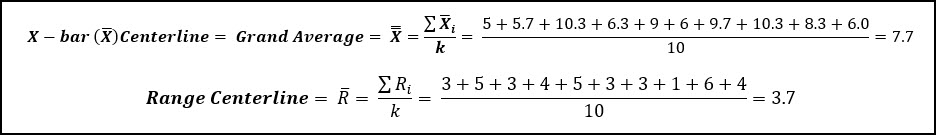
We can also calculate the control limits for the Range Chart:

We can now use the grand average (7.7) and R-bar (average range value) to calculate the control limits for the x-bar chart.

X-bar & S Charts

The X-bar and S Chart is similar to the X-bar and R chart in that the subgroup average(X-bar) is used to monitor the central tendency of the data.

When the subgroup sample size (n) gets larger than 10 samples, the range of the sub-group becomes a less reliable estimate of the processes variability and the sub-groups standard deviation becomes a more representative parameter of variation.

In switching from the Range to the Standard Deviation this control chart becomes more effective at detecting smaller levels of special cause variation within the data.  Recall that the sub-group sample standard deviation is calculated as such:

The drawback in this switch from the range to the standard deviation is that it is more difficult to implement and maintain due to the calculations required for the standard deviation value.

The one thing that doesn’t change with the X-bar and S chart is the way we calculate our grand average for the X-bar chart:

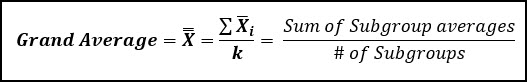
What does change is the way we calculate our control limits for X-bar.

You’ll notice instead of the range, we’re using a new parameter called s-bar which is the average standard deviation across all sub-groups. This is multiplied by a factor (A3). You can see the s-bar calculation below:

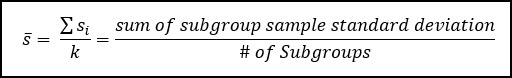
We use the average standard deviation (s-bar) to also calculate the control limits for the S Chart. These factors (B4 & B3) can be found on the table below and are based on the subgroup size (n).

Just like the grand average is a good estimate of the population mean (μ), you can also use your s-bar value to calculate an unbiases estimate of the population standard deviation using a constant (c4) which is also on the table below.

 

X-Bar and S Chart Constants

Below are the constants that must be used to calculate the critical elements (CL, UCL, LCL) of the X-bar and R chart.

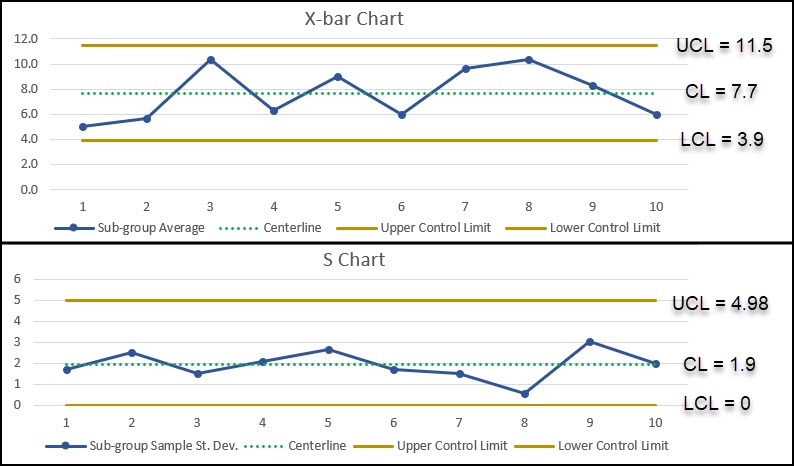
X-Bar and S Chart Example

Let’s use the data from the previous example to see what our X-bar and S chart would look like.

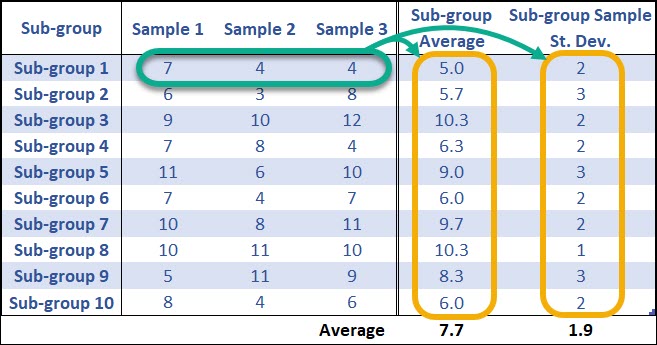
Nothing changes about the way we calculate the grand average (centerline of the X-bar graph).

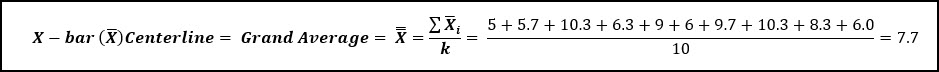
What does change is the way we use the sample standard deviation for each sub-group to calculate the average sample standard deviation, which is used to create the control limits for the X-bar graph. We will also use different constants to calculate these values.

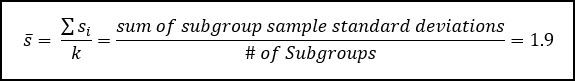
We can also calculate the control limits for the S Chart:

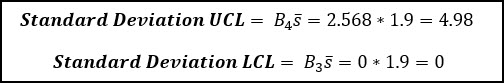
We can now use the grand average (7.7) and R-bar (average range value) to calculate the control limits for the x-bar chart.

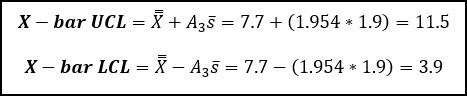
You’ll notice that these control limits are identical to what we calculated above from the X-bar and R example.

I-MR Charts

The I-MR control chart is meant to be utilized when your subgroup is only a single observation (n = 1).

This chart is useful in situations where it is costly to collect data or if production volumes are very low, or any other situation where data is in short supply or collected infrequently (monthly data) such as calibration data.

This control chart is called the Individual (I or X) chart and it is paired up with a Moving Range (MR) chart to measure the process variation.

The benefits of an I chart is that it’s easy to use and understand. The downside is that it’s not as sensitive to shifts in the process as other charts, and the control chart is very sensitive to the underlying assumption of normality.

The moving range is the difference between n consecutive points. Usually, for the MR chart, n = 2, thus we’re looking at the absolute difference between the last 2 consecutive values.

However, the moving range can be based on n = 4, where we calculate the range of the preceding 4 data points.

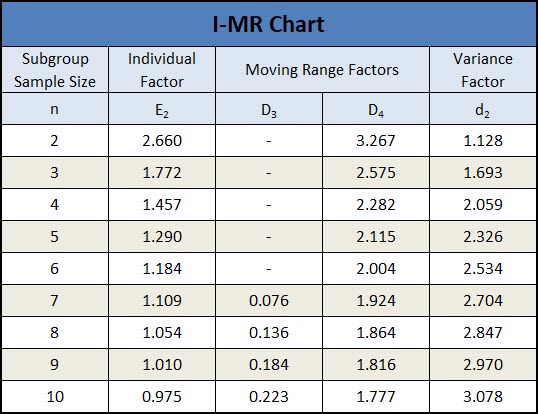
Below is a table showing each of the calculations required for an I-MR Control Chart.

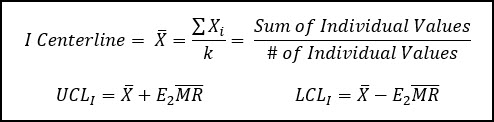
The Moving Range value is calculated as the difference between multiple (n) consecutive data points. Additionally, the control limits for the MR are calculated using constants D4 & D3.

I-MR Chart Example

Let’s say you’re monitoring the temperature of your process, and you collect a single value every hour. Let’s analyze that data to see if our process is in control.

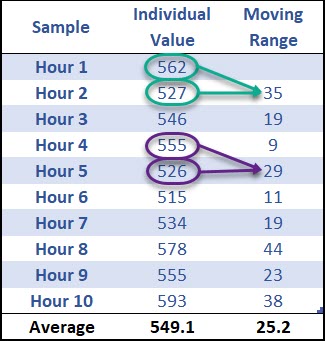
The first thing to understand is how to calculate the Moving Range, which depends on the number of samples you’d like to analyze within your moving range.

In this example n = 2 for the moving range, which means we’re calculating the absolute value of the current observation minus the previous observation.

There is no moving range for hour 1, but for hour 2 we take the individual value (527), and subtract from the previous hour (562), and take the absolute value.

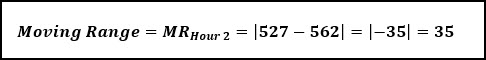
Now we can calculate the Centerline and Control Limits for the Individual Chart and Moving Range Chart.

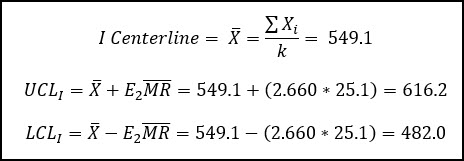
The centerline for the moving range chart is calculated as the average moving range value, and the control limits are calculated using the D4 & D3 factors, which can be found in the table above.

For this example, n = 2, which means we’ve calculated our moving range value by only considering 2 consecutive points in a row.

Let’s see what this looks like graphically:

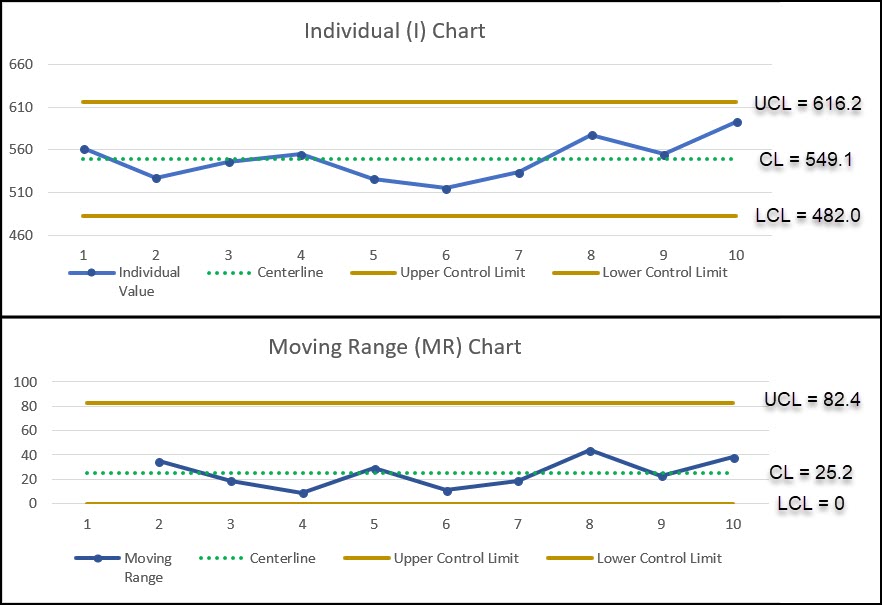
You can see that all of the data points on the individuals chart and moving range chart are all within the control limits calculated previously. Thus, the process appears to be in a stable state.

That about wraps it up for the variable control charts.

Let’s switch gears and talk about attribute control charts.

Attribute Control Charts

There are 4 control charts for attribute (Discrete) data that we will cover.

Unlike variable control charts, these discrete data control charts are only a single chart. It’s not like the X-bar and R chart where there’s two charts, one for the average and the other for the variance. With discrete data it’s a single chart.

A quick general comment, attribute control charts are normally easier to construct and execute, however they tend to be less sensitive to small changes in variation or process shifts.

How to Choose the Right Attribute Control Chart

The first big distinction between these four charts is the whole defect v. defective discussion from above.

The c chart & u charts analyze defects over time, while the p chart & np chart analyze defectives over time.

The second big distinction between these four charts is the sample size associated with the control chart and whether that sample size is constant or variable.

When the sample size is constant between subgroups we use the c chart & np chart and the math is much easier. When the sample size varies we use the p chart and the u chart and the math gets a bit more difficult.

You can see this in the matrix below.

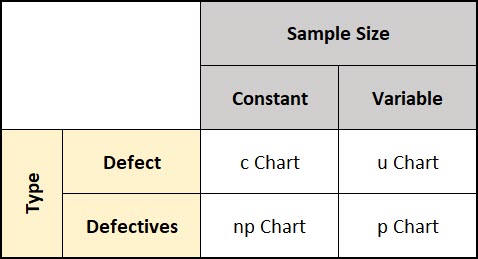
You can pick the proper control chart by considering these two factors. Are you analyzing defects or defectives, and will you take a constant sample size, or will the sample size vary.

Let’s review each chart type individually.

• p-Chart: Trending of Defectives with a Variable Sample Size
• np-Chart: Trending of Defectives with a Constant Sample Size
• u-Chart: Trending of Defects with a Variable Sample Size
• c-Chart: Trending of Defects with a Constant Sample Size

np & p Charts trend the number of Defectives and the math is based on the Binomial distribution which operates under the assumption that every unit inspected can only be counted as “bad” one time.

u & c Charts utilize the Poisson distribution because they trend the number of defects where it is possible for each item inspected to contain multiple defects.

Let’s jump into these individually and start with the p chart.

The p Chart

The p chart trends the proportion (p) of defective items across time when the sampling size varies.

This chart is the most sensitive of the attribute control charts to any changes in your process.

Instead of proportion defective, you’ll might see this called the fraction defective.  Also, just to confuse you even more, people also interchange the word defective with nonconforming items. So, you might also see fraction nonconforming.

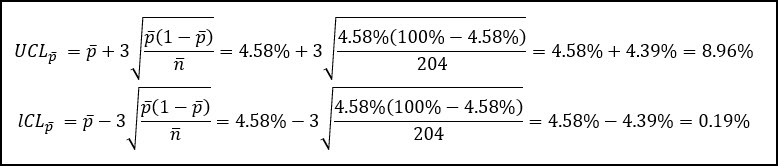
I’m going to stick with proportion defective, and you can see how we calculate the centerline and control limits below.

The centerline is the average proportion defective, which we calculate by taking the sum total of all defective items and divide that by the total number of units inspected across all subgroups.

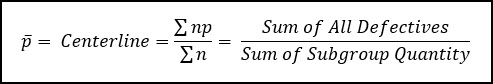
We can then use that average proportion defective to calculate the control limits:

The confusing part about the p chart is that it is possible to have different control limits based on your different sample sizes.

However, a common approach is the create control limits using the average sample size (n-bar) which is what’s shown above.

Then if you see any data points that are near (above or below) those control limits, you can recalculate the control limits for that exact sub-group to see if the process is truly out of control or not.

Other common approaches include putting two limits on the chart, one for the smallest sample size expected, and one for the largest sample size expected, then evaluating points that fall in between those two limits.

p Chart Example

Let’s work through an example where you’ve measured 15 lots (subgroups) where each lot has a different sample size and you’ve counted the number of defective units from each lot.

You can see that each subgroup (lot) has a different percentage defective.

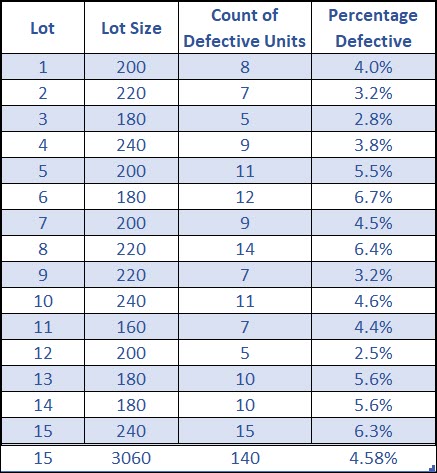
Let’s calculate the control limits and compare these percentage defectives against them to see if our process is in control.

Let’s start by calculating the average proportion defective, which is the total number of rejects (140), divided by the total number of units inspected (3060).

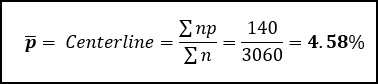
We can also calculate the average number of samples per subgroup, n-bar, by taking the total number of samples inspected and dividing by the number of subgroups (k = 15).

We can now use those two values to calculate our upper and lower control limits.

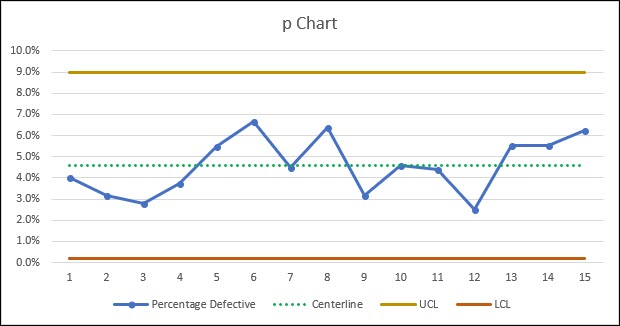
Based on these control limits, our process appears to be stable and in control.

Our process still has an average percentage of defective items of 4.58%, which isn’t great, but at least we’re in control.

The np Chart

The NP-Chart is a variant of the P-chart where we have the luxury of a constant sample size, which makes the math easier.

When we have a constant sample size the control chart is able to trend the number of defectives units (NP) without having to normalize by the fluctuating sample size.

In the equations below, n is the sample size, which will be constant, p-bar is the average fraction defective, and k is the number of sub-groups being analyzed.

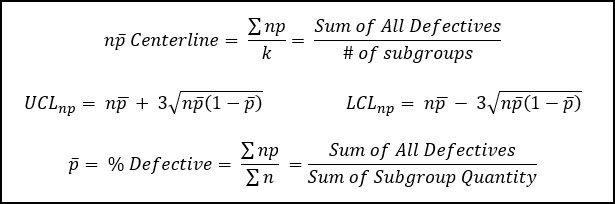
np Chart Example

Ok, let’s use the following data from 15 sub-groups to see how an NP chart would come together. For each lot the sample size is constant at 120 units, and we’ve counted the number of defective units within each subgroup.

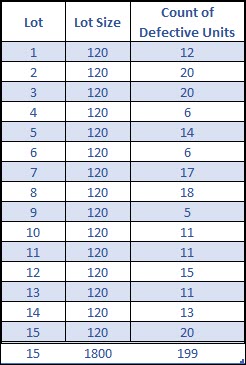
The average of the process can be calculated as such:

The average percentage defective (p-bar = 11.06%) is also equal to the number of defect units per subgroup (13.27), divided by the number of samples per sub-group (120).

Then we can calculate the control limits using this information:

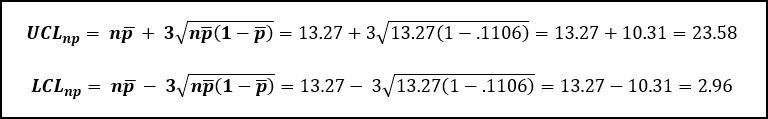
Graphically, this looks like this:

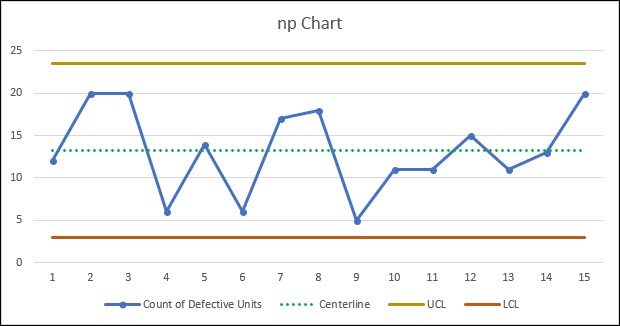
Based on this information our process appears to be in control and stable with no single sub-group having a count of defective items greater than our upper control limit of 23.58 (23), or less than the lower control limit of 2.96.

The c Chart

Let’s switch gears away from the p chart and np chart and move on to the c chart and u chart.

Remember, the p and np charts were monitoring defective items, while the c and u chart monitor defects, and it is possible to have multiple defects per defective unit.

Thus, it might be possible to have more defects than the number of samples you’re inspecting – granted this would be an awful process!

The c-chart should be utilized when trending the number of defects per unit when your sample size is constant. The c stands for “Count” as we’re simply counting the number of defects per inspection.

In this situation the process average (Centerline) is simply the average number of defects per inspection, where each inspection is considered a unique sub-group.

Below are the calculations for the centerline and control limits where k is the total number of subgroups being analyzed.

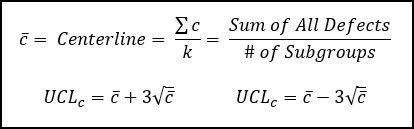
c Chart Example

Imagine the following situation where you have inspected 1,500 units per sub-group (lot), and you’re counting the number of defects per sub-group (lot).

Because the sample size is constant, and we know we’re counting defects, we should use the c-chart.

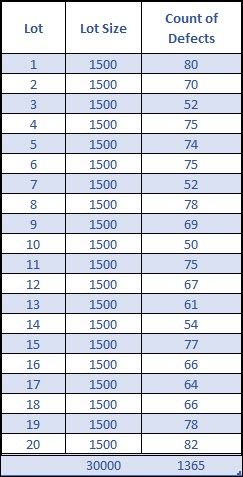
Let’s start by calculating the center (centerline) of our process:

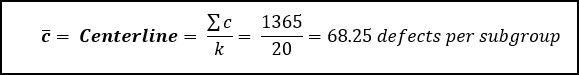
Then we use this average number of defects per subgroup to calculate the control limits:

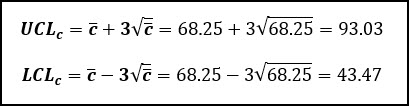
Graphically, this looks like this:

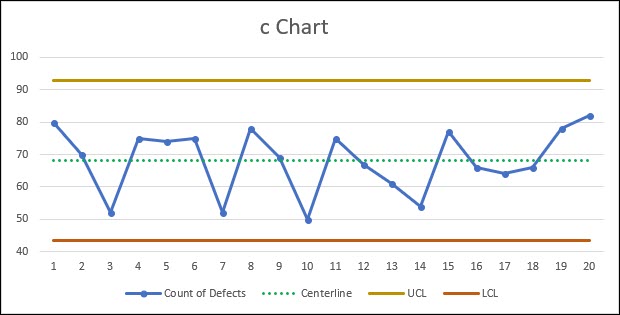
Again, because the count of defects per sub-group never fall outside of our control limits, our process appears to be in a state of statistical control.

The u Chart

Alright, on the last control chart – the u chart.

Similar to the c chart, the u chart controls for the percentage of defects per subgroup and can accommodate a variable sample size.

The u chart normalizes the number of defects by the subgroup sample size, thus trending the number defects per sub-group.

This chart is similar to the P Chart which also allows for a varying sample size, and similarly, the control limits are dependent on the sample size (n).

Thus, you can calculate a control limit for every sample size, or if you have standard sample sizes you can calculate multiple control limits for your more frequently expected sample sizes.

We calculate the process average (centerline), by finding the average number of defects per unit inspected.

u Chart Example

Let’s look at an example similar to the p chart, where we’ve inspected 15 sub-groups (lots), and the lot size can vary, and we’ve counted the number of defects observed.  We then calculate percentage of defects for each subgroup.

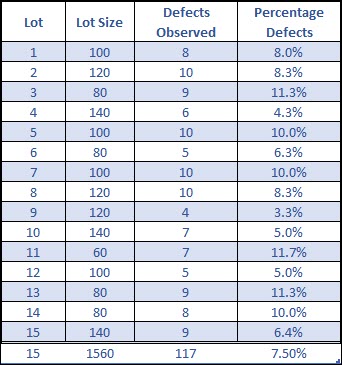
The centerline of the process is the overall average percentage of defects.

We can also calculate the average number of samples per subgroup, n-bar, in order to calculate our upper and lower control limit.

Remember that the u chart has the flexibility to calculate a different control limit for each sub-group, based on that sub-groups sample size. However, oftentimes n-bar is used to simplify this calculation.

If you want to calculate the control limits for each sample size, simply use the same formula, but instead of n-bar, us n (units per subgroup) for each unique sub-group.

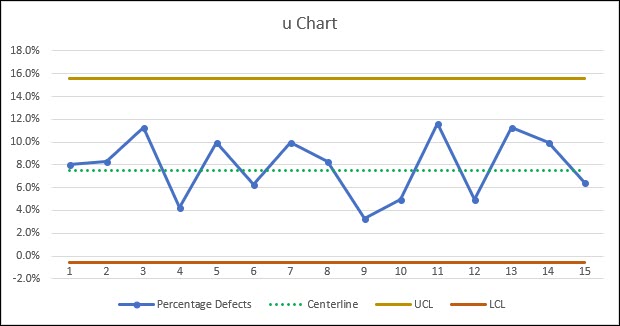
Similar to other control charts above, this process appears to be in a state of statistical control, as none of our data points fall outside of the calculated control limits.

Analyzing & Interpreting Control Charts

Ok, so with all of the control charts above, I’ve been concluding that each of these processes is in control because none of the points fall outside of the calculated control limits.

However, there is more analysis that you can do to your control chart to determine if special cause variation is present.

Remember, the overall goal of a control chart is to help you in identifying special causes of variation, and ultimately improving your process for better performance.

Let’s review the 8 rules that can be used to determine if a process is in a state of statistical control.

The 8 Rules for statistical control

Ok, so let’s assume you’ve picked a control chart, and you’re monitoring that data, now it’s time to analyze the data to make sure your process is in control.

A handful of rules have been developed to assist you in concluding that your process under the influence of a special cause of variation, and thus is out of statistical control.

Before we review the rules, you have to understand the different zones of a control chart. These zones are created utilizing the standard deviation of your data:

• Zone C is the area between the centerline (process average) and the 1st standard deviation
• Zone B is the area between the 1st standard deviation and 2nd standard deviation
• Zone A is the area between the 2nd standard deviation and 3rd standard deviation

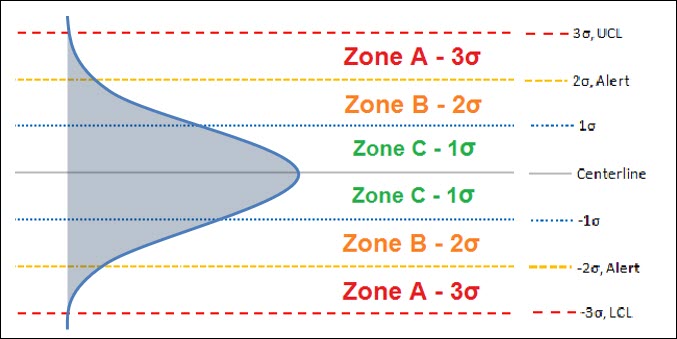
Utilizing these Zones, we’re able to create rules to identify special causes of variation:

• Rule 1 – Any single data point outside of either the upper or lower control limits (>3σ) – outside Zone A.
• Rule 2 – Two out of three consecutive data points in Zone A (same side) – greater than 2σ, but less than 3σ.
• Rule 3 – Four out of Five consecutive data points in Zone B (same side) – greater than 1σ, but less than 2σ.
• Rule 4 – Eight or more consecutive points on either side of the Centerline –a run
• Rule 5 – Six points in a row, all increasing or decreasing – a trend
• Rule 6 – 14 points in a row, alternating up and down – systematic variation
• Rule 7 – 15 points in a row within Zone C (<1σ) – to little variation
• Rule 8 – 8 points in a row outside of Zone C (>1σ) on either side

Violating any one of these rules can be a strong indication that your process is under the influence of a special cause variation and that further investigation is needed.

Let’s now jump over to some of the common errors that occur when analyzing a control chart.

4 Common Control Chart Analysis Errors

Control charts are oftentimes some of the most useful tools we can use to help create a stable production process and improve quality.

However, if used incorrectly, control charts can cause issues that are costly.

Below are 4 most common errors that people make when analyzing their control charts:

The first, and most common mistake is called the Re-Sampling Fallacy.

This error occurs when you don’t trust an out of control measurement and instead of analyzing their process and making adjustments, you re-sample from the process which can result in you missing the initial signal of an out of control process.

The second most common mistake is described as an Under-Adjustment.

Under-adjustment occurs most often due to a lack of inattention to the control chart data or a lack of caring. Either of these issues may allow for an out of control process to continue running without correction.

The third most common mistake is described as the Over-Adjustment.

This is possibly the most common mistake that occurs and oftentimes it is a result of a well-intentioned operator who makes an adjustment anytime a process is not perfectly on center.

In many cases, people will make adjustments to the process when the right decision is to conclude that any variation is normal to the process and that an adjustment will not make the process better.

The final mistake occurs when using the variable control charts, and not starting your analysis with the Range Chart.

When special cause variation occurs, it can often affect the variability chart (Range or Standard Deviation) and the Average values.

People often start by looking at the average value, but the proper place to start is with the range chart.

Remember, the range values are used to calculate the control limits on the average chart. So, if the range data is out of control, your limits on the average chart can often be wrong.

PRE-Control Charts

Okay, we’re almost done!

Let’s wrap up with two quick sessions on pre-control charts, then we will move on to short run SPC.

Ok, so pre-control charts are somewhat controversial in that they are created using the specification limits discussed earlier, and thus it does not reflect the voice of the process.

The pre-control chart simply monitors the center of your process to make sure it’s on target. This tool is highly sensitive to the assumption of normality, and only works if your process has good process capability (Cpk).

The way to create a pre-control chart is to take your specification range and create pre-control boundaries. These PC boundaries are often 25%, 15% or even as small as 7% of your overall specification range.

Let’s take the example below where you’re creating a widget whose length is 6.00” +/- 0.25”. This means your USL (upper specification limit) is 6.25” and your lower specification limit is 5.75”.

Now let’s create our PC Boundaries at 25% of the total tolerance on either side. So, if the total tolerance range is 0.50, then our PC lines would be set at 25% of that, which is 0.125”.

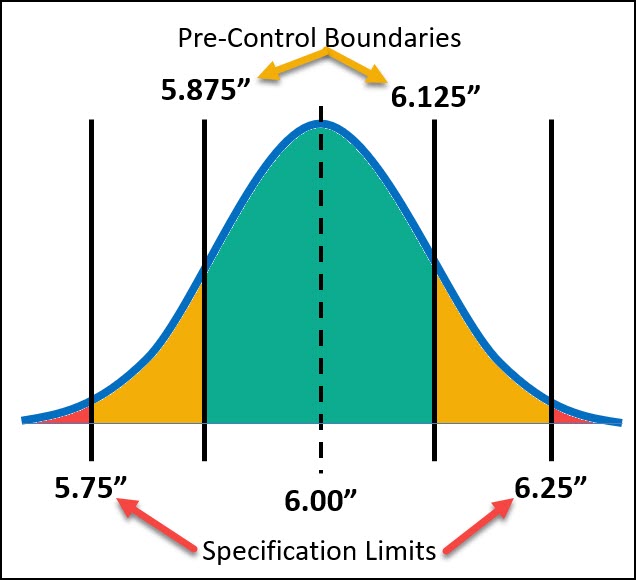
The specification limits, PC boundaries and target create 3 different zones – Green, Yellow and Red.

The red zone is any part that falls outside the specification limits. The Green Zone is the safe area and it’s the middle of your distribution. The Yellow Zone is the space between the P-C Line and the specification limit.

These lines are used to make different decisions when starting up a process.

If consecutive parts are produced within the green area, your process can proceed. If you’re in the red area, you need to make adjustments. If you have consecutive parts in the yellow area, you have to adjust the process back to center.

As you can see, this pre-control chart is very different than the control charts already discussed. In fact, there’s no real “chart” at all, you’re simply comparing measurements against the specification limits.

The advantage of this type of tool is that it’s easy to implement and can help to keep your process on center.  This tool is also a great way to make sure your process is setup correctly before starting.

The downside is that these charts can miss subtle shifts in your process and they don’t reflect the natural variation in your process. Additionally, this tool losses value if your process is not already stable and capable.

Short-Run SPC

Ok – we’re on to the last topic – short run SPC.

One thing that hasn’t yet been said but is important is that the control charts above are only effective and appropriate for long term, continuous production runs.

These charts don’t work for short, infrequent production runs.

Luckily, short-run SPC can help you monitor and control processes that are infrequent or short in nature.

Similar to above, there are short run SPC charts for both attribute and variable data.

One of the most common approaches in short run SPC is the standardized control chart, where are sub-group averages are normalized to find the z-value associated with each sub-group. Then the Z score is control charted.

Below is an example of the short run version of the u-chart, where we will calculate a Z score for ever sub-group.

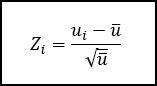
This is similar to other z-transformations that we’ve performed. We subtract the individual value (ui) by the mean value (u-bar, then divide by the standard deviation (square root of u-bar).

The centerline of this type of short run SPC chart is zero. If a process is on target, the individual value (ui) will be equal to the mean (u-bar) and thus the z-transformation will be equal to zero.

Then when we plot these transformed values, our upper and lower control limits become +3 and -3, which are the z-transformations associated with being 3 standard deviations away from the mean.

This same approach is applicable to other attribute control charts.

This is just an example of a single type of short run SPC chart – I won’t go into detail about any other types of charts as they are out of scope of the CQE body of knowledge.

Conclusion

Oh man, what a big chapter!!!

If you made it this far – super congrats!

Ok, so let’s wrap up quickly with a quick review of the major topics discussed.

There were 8 major topics covered in this chapter.

The first is the objectives and benefits of SPC, which primarily involve around the ability to distinguish between common and special cause variation. Having this ability allows you to eliminate special cause variation and improve the stability of your process over time.

This led us into the second section which was in in-depth conversation about those two types of variation – common cause variation and special cause variation.

The third section is how to select the proper variable to include in a control chart. This included a discussion about variable versus discrete data, and the difference between a defect and a defective.

The fourth section was probably the most over-looked topic within control charting and that’s the idea of a rational subgroup.

The fifth section is the meat of the entire chapter, and it covers the construction and use of various control charts. It includes 3 variable control charts and 4 attribute charts.

For variable charts, we covered the I-MR, the X-bar & R, and the X-bar and S chart. For attribute charts, I’ll explain the p-chart, np-chart, c-chart and u-chart.

The sixth section is the analysis of control charts. Which includes 8 rules for statistical control.

The seventh and eighth sections covered the concepts of pre-control charts and short-run SPC. These were both very brief introductions to these topics.