Statistical Quality Control

Statistical Quality Control

Controlling and improving quality is an important strategy for an organization since the quality provides a competitive advantage to the organization. The organization which delight its customers by improving and controlling quality, can dominate its competitors. Hence the main objective an organization is to achieve quality assurance so that it can not only satisfy its customers but also delight them.

With the advent of industrial revolution in the nineteenth century, mass production replaced manufacturing in small shops by skilled craftsman and artisans. While in the small shops the individual worker was completely responsible for the quality of the work, this was no longer true in mass production where the contribution each individual worker towards the finished product only constituted an insignificant part in the total process. The quality control in the large organization was achieved with the help of quality inspectors responsible for checking the product quality with the 100 % inspection of all the important characteristics.

In order to achieve this objective, different statistical techniques have been developed, which are useful for controlling the quality of products with respect to the specifications or standards. The practice of controlling product quality against the specifications using statistical tools is known as ‘statistical quality control’ (SQC). SQC is to be viewed as a kit of techniques which can influence decisions to the functions of specification, production, or inspection.

SQC is defined as the technique of applying statistical methods based on the theory of probability and sampling to establish quality standard and to maintain it in the most economical manner. It is an economic and effective system of maintaining and improving the quality of outputs throughout the whole operating process of specification, production, and inspection based on continuous testing with random samples.

Quality control includes quality of product or service given to customer, leadership, commitment of the management, continuous improvement, fast response, actions based on facts, employee participation and a quality driven culture. Objective of SQC is to control (i) the material reception, internal rejections, and clients claims, (ii) evaluations of the same, and (iii) corrective actions and their follow-up. These systems and methods guide all quality activities. The development and use of performance indicators is linked directly or indirectly to the customer requirements and satisfaction as well as to the management.

SQC is one of the techniques for the scientific management. The principle of quality control by the statistical techniques covers almost all aspects of production, i.e. quality of materials, quality of man power, quality of machines, and quality of management.

SQC refers to the use of statistical methods in the monitoring and maintaining of the quality of products and services. It is the term used to describe the set of statistical techniques employed by quality professionals for evaluating the quality. The three words included in SQC are described below.

Statistics – It is science which deals with the collection, classification, analysis, and making of inferences from data or information. It means availability of good amount of data to obtain reliable results. Statistics handles the data in order to draw the conclusions using various techniques.

Quality – It is a relative term and is normally explained with reference to the end use of the product. Quality is hence defined as fitness for purpose.

Control – Control is a system for measuring and checking or inspecting a phenomenon. It suggests when to inspect, how frequently to inspect and how much to inspect. Control ascertains quality characteristics of an item, compares the same with prescribed quality characteristics of the item, compares the same with prescribed quality standards, and separates defective item from non-defective ones.

The data for SQC can be collected in several ways namely (i) direct observation, and (ii) indirect observations. Data on quality characteristics are categorized as (i) continuous variable data which can assume any number on continuous scale within a range, and (ii) discrete attributes which are the count of an event and which assume a finite or countable infinite number of values.

Dr. Walter A. Shewhart a researcher of Bell Telephone Laboratories (a Research and Development Unit of the American Telephone and Telegraph Company) is called the father of quality control analysis. He developed the concepts of SQC. In 1924, for the purpose of controlling quality, he developed charting techniques and statistical procedures for controlling in-process manufacturing operations. His statistical procedures are based on the concept of independent and identically distributed random variables. Based on these concepts, he distinguished between chance causes, producing random variation intrinsic to the process, and assignable causes which one is to look for and take needed corrective actions. In order to identify the assignable causes, he recommended 3 sigma (standard deviation) limits above and below the mean value of the variable. Observations beyond these limits were then used to identify the assignable causes. This is normally considered as the beginning of SQC.

Variation is a fact of nature and manufacturing processes are not exceptions to this. Types of variation can be (i) within the product, (ii) among the products produced during the same period of time, and (iii) among the products produced at different period of time. The probability of an event describes the chance of occurrence of that event. The fundamental basis of SQC is the theory of probability.

According to the theories of probability, the dimensions of the components made on the same machine and in one batch (if measured accurately) vary from component to component. This can be due to inherent machine characteristics or the environmental conditions. The chance or condition that a sample represents the entire batch or population is developed from the theory of probability. Relying itself on the probability theory, SQC evaluates batch quality and controls the quality of the processes and the products.

SQC uses three scientific techniques, namely (i) sampling inspection, (ii) analysis of the data, and (iii) control charting. It can be divided into following three broad categories namely (i) descriptive statistics, (ii) statistical process control, and (iii) acceptance sampling.

Descriptive statistics are the statistics used to describe certain quality characteristics such as the central tendency and variability of the observed data. It also describes the relationship. Descriptive statistics include statistics such as the mean, standard deviation, the range, and a measure of the distribution of data.

Statistical process control (SPC) consists of statistical techniques which involve inspecting a random sample of the output from a process and deciding whether the process is producing products with characteristics which fall within a predetermined range. SPC answers the question whether the process is functioning properly or not. These techniques are very important for a process since they help in identifying and catching a quality problem during the production process.

When inspection is for the purpose of acceptance or rejection of a product, based on adherence to a standard, the type of inspection procedure employed is normally called acceptance sampling. Acceptance sampling helps in evaluating whether there is problem with quality and whether desirable quality is being achieved for a batch of product. Acceptance sampling consists of the process of randomly inspecting a sample of goods and deciding whether to accept the entire lot based on the results. This sampling decides whether a batch of goods is to be accepted or rejected.

Terms used in SQC

The following are some of the terms used in the SQC technique.

Mean – It is an important statistic tool which measures the central tendency of a set of data. The mean is computed by simply summing up of all the observations and dividing by the total number of observations.

Range and standard deviation – This information provides with the variability of the data. It tells how the data is spread out around the mean. Range is the difference between the largest observation and the smallest observation in a set of data while standard deviation is a statistics which measures the amount of data dispersion around the mean. Small values of the range and standard deviation mean that the observations are closely clustered around the mean while large values of the range and standard deviation mean that the observations are spread around the mean.

Distribution of data – It is a measure to determine the quality characteristics. When the distribution of data is symmetric then there are same numbers of observations below and above the mean. This is what is normally found when only normal variation is present in the data. When a disproportionate number of observations are either above or below the mean, then the data has a skewed distribution.

Population – It is the set of all items which possess a certain characteristic of interest. Parameter is a characteristic of a population, something which describes it. Sample is a subset of a population.

Statistic – It is a characteristic of a sample, used to make inferences on the population parameters which are typically unknown.

Accuracy and precision – Accuracy is the degree of uniformity of the observations around a desired value. Precision is the degree of variability of the observations.

Basic SQC techniques

There are a number of diagnostic techniques available to the quality control personnel for investigating the quality problems. There are seven basic techniques employed for SQC. These basic techniques are (i) check sheets, (ii) histograms, (iii) Pareto analysis, (iv) control chart, (v) cause and effect diagram, (vi) stratification, and (vii) scatter diagram.

The seven basic techniques of quality is a designation given to a fixed set of graphical techniques identified as being most helpful in trouble shooting issues related to quality. These techniques are called basic since they are suitable for people with little formal training in statistics and since they can be used to solve the vast majority of quality related issues.

The seven basic SQC problem solving techniques are used routinely to identify improvement opportunities and to assist in reducing variability and eliminating waste. They can be used in several ways throughout the DMAIC (define, measure, analyze, improve, and control) problem solving process which is a data driven quality strategy used to improve processes.

Check sheets

In the early stages of process improvement, it becomes frequently necessary to collect either historical or current operating data about the process under investigation. This is a common activity in the measure step of DMAIC. A check sheet can be very useful in this data collection activity. The check sheet was developed by an aerospace company engineer who was investigating defects which occurred on one of the company’s tanks. The engineer designed the check sheet to help summarize all the historical defect data available on the tanks. Because only a few tanks were manufactured each month, it seemed appropriate to summarize the data monthly and to identify as many different types of defects as possible. The time-oriented summary is particularly valuable in looking for trends or other meaningful patterns.

When designing a check sheet, it is important to clearly specify the type of data to be collected, the part or operation number, the date, the analyst, and any other information useful in diagnosing the cause of poor performance. If the check sheet is the basis for performing further calculations or is used as a worksheet for data entry into a computer, then it is important to be sure that the check sheet is adequate for this purpose. In some cases, a trial run to validate the check sheet layout and design can be helpful.

Check sheets are simple data gathering devices. They are used to collect data effectively and efficiently. They prepare data for further analysis. A check sheet is in the form of a designed format used to collect data in a systematic manner and in real time at the location where the data is generated. The data it captures can be either quantitative or qualitative. When the information is quantitative, the check sheet is sometimes called a tally sheet. The defining characteristic of a check sheet is that data are recorded by making marks (checks) on it. A typical check sheet is divided into regions, and marks made in different regions have different significance. Data are read by observing the location and number of marks on the sheet. Various types of check sheets are (i) process distribution check sheet, (ii) defect cause check sheet, (iii) defect location check sheet, and (iv) defect cause-wise check sheet.

Histogram

A histogram is a graphical representation (bar chart) of the distribution of data. It is an estimate of the probability distribution of a continuous variable and was first introduced by Karl Pearson. A histogram is a representation of tabulated frequencies, shown as adjacent rectangles, erected over discrete intervals (bins), with an area equal to the frequency of the observations in the interval. The height of a rectangle is also equal to the frequency density of the interval, i.e., the frequency divided by the width of the interval. The total area of the histogram is equal to the number of data.

A histogram can also be normalized displaying relative frequencies. It then shows the proportion of cases which fall into each of several categories, with the total area equaling one. The categories are normally specified as consecutive, non-overlapping intervals of a variable. The categories (intervals) are to be adjacent, and are frequently chosen to be of the same size.http://en.wikipedia.org/wiki/Histogram#cite_note-2 The rectangles of a histogram are drawn so that they touch each other to indicate that the original variable is continuous. Histograms are used to plot the density of data, and frequently for density estimation which is the estimating the probability density function of the underlying variable. The total area of a histogram used for probability density is always normalized to one.

A histogram is a compact summary of data. To construct a histogram for continuous data, it is necessary to divide the range of the data into intervals, which are normally called class intervals, cells, or bins. If possible, the bins are to be of equal width to improve the visual information in the histogram. Some judgment is to be used in selecting the number of bins so that a reasonable display can be developed. The number of bins depends on the number of observations and the amount of scatter or dispersion in the data. A histogram which uses either too few or too many bins is not informative. Normally between 5 bins and 20 bins are considered satisfactory in most cases and that the number of bins increases with the number of observations. Choosing the number of bins approximately equal to the square root of the number of observations frequently works well in practice.

Once the number of bins and the lower and upper boundary of each bin have been determined, the data are sorted into the bins and a count is made of the number of observations in each bin. To construct the histogram, the horizontal axis is used to represent the measurement scale for the data and the vertical scale to represent the counts, or frequencies. Sometimes the frequencies in each bin are divided by the total number of observations, and then the vertical scale of the histogram represents relative frequencies. Rectangles are drawn over each bin and the height of each rectangle is proportional to frequency (or relative frequency).

Histograms are used to understand the variation pattern in a measured characteristic with a reference to location and spread. They give an idea about the setting of a process and its variability. Histograms indicate the ability of the process to meet the requirements as well as the extent of the non conformance of the process. Different patterns of histogram are shown in Fig 1.

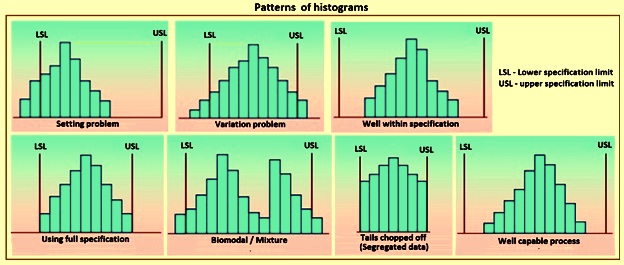
Fig 1 Patterns of histogram

Pareto chart

In general, the Pareto chart is one of the most useful of the seven techniques of SQC. Its applications to quality improvement are limited only by the ingenuity of the analyst The Pareto chart is simply a frequency distribution (or histogram) of attribute data arranged by category. Pareto charts are frequently used in both the measure and analyze steps of DMAIC.

Ideally people want to focus their attention on fixing the most important problem. Pareto chart is a simple and formal technique which helps to identify the top portion of the causes which are to be addressed to resolve the majority of the problems. It is a decision making technique which statistically separates a limited number of input factors as having the greatest impact on an outcome, either desirable or undesirable. In its simplest terms, Pareto chart typically shows that a disproportionate improvement can be achieved by ranking various causes of a problem and by concentrating on those solutions or items with the largest impact. The basic principle is that not all inputs have the same or even proportional impact on a given output.

Pareto chart is also referred as the ‘80 / 20 rule’. Under this rule, it is assumed that 20 % of causes when addressed to, generate 80 % of the results. The technique of the Pareto chart is used to find the 20 % of those causes which when addressed resolves 80 % of the problems. This ratio is merely a convenient rule of thumb and is not to be considered as law of nature.

For illustrating a Pareto chart, the defect data of a fuel oil storage tank is considered here. Plotting the total frequency of occurrence of each defect type against the various defect types produces a Pareto chart. Through this chart, the user can quickly and visually identify the most frequently occurring types of defects. Hence, the causes of these defect types probably are to be identified and attacked first. It is to be noted that the Pareto chart does not automatically identify the most important defects, but only the most frequent. For example, casting voids occur very infrequently (e.g. 3 out of 170 defects, or 1.8 %) in the above example. However, voids can result in scrapping the tank, a potentially large cost exposure. Perhaps is is so large that casting voids are to be elevated to a major defect category.

When the list of defects contains a mixture of those which can have very serious consequences and others of much less importance, one of two methods can be used. These methods are (i) use a weighting scheme to modify the frequency counts, and (ii) accompany the frequency Pareto chart analysis with a cost or exposure Pareto chart. There are many variations of the basic Pareto chart as given below.

Fig 2a shows a Pareto chart applied to an electronics assembly process using surface-mount components. The vertical axis is the percentage of components incorrectly located, and the horizontal axis is the component number, a code which locates the device on the printed circuit board. It can be seen that the locations 28 and 40 account for 70 % of the errors. This can be the result of the type or size of components at these locations, or of where these locations are on the board layout.

Fig 2b shows another Pareto chart from the electronics industry. The vertical axis is the number of defective components, and the horizontal axis is the component number. It can be seen that each vertical bar has been broken down by supplier to produce a ‘stacked Pareto chart’. This analysis clearly indicates that supplier 1 provides a disproportionately large share of the defective components.

Pareto charts are widely used in the non-manufacturing applications of quality improvement methods. Fig 2c shows a Pareto chart used by a quality improvement team in a procurement department of the organization. The team was investigating errors on purchase orders in an effort to reduce the number of purchase order changes of the organization. Each change typically cost between USD 100 and USD 500, and the organization has issued several hundred purchase order changes each month. This Pareto chart has two scales namely (i) one for the actual error frequency and (ii) another for the percentage of errors.

Figure 2d presents a Pareto chart constructed by a quality improvement team in the continuous casting department to reflect the reasons for the rejections of the cast slabs.

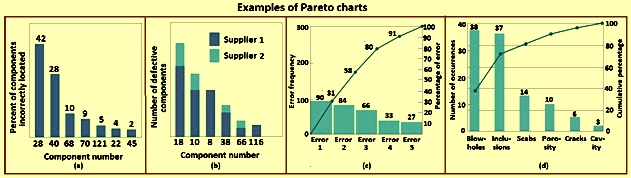
Fig 2 Examples of Pareto charts

Pareto chart is a creative way of looking at causes of the problems since it helps stimulate thinking and organize thoughts. However, it can be limited by its exclusion of possibly important problems which can be small initially, but which grow with time. It is to be combined with other analytical tools such as failure mode and effects analysis and fault tree analysis for example. The application of the Pareto chart in risk management allows management to focus on those risks which have the most impact.

Control chart

A control chart is a graph which shows whether a sample of data falls within the common or normal range of variation. A control chart has upper control limit (UCL) and lower control limit (LCL) which separate common from assignable causes of variation. The UCL is the maximum acceptable variation from the mean for a process which is in a state of control while the LCL is the minimum acceptable variation from the mean for a process which is in a state of control. The common range of variation is defined by the use of control chart limits. Control limits are calculated from the process output data and they are not the specification limits. A process is out of control when a plot of data reveals that one or more samples falls outside the preset control limits. Hence by using the control charts, one can know from graphic picture that how the production is proceeding and where corrective action is needed and where it is not needed.

The control chart is a very useful process monitoring technique. When unusual sources of variability are present, sample averages gets plotted outside the control limits. This is a signal that some investigation of the process is to be made and corrective action to remove these unusual sources of variability is to be taken. Systematic use of a control chart is an excellent way to reduce variability.

The general theory of control charts was first proposed by Walter A. Shewhart, and control charts developed according to these principles are frequently called Shewhart control charts. The control chart is a graphical display of a quality characteristic which has been measured or computed from a sample against the sample number or time. The chart contains a centre line which represents the average value of the quality characteristic corresponding to the in-control state. That is, only chance causes are present. Two other horizontal lines, called the UCL and the LCL are also shown on the chart.

A typical control chart is shown in Fig 3. This chart plots the averages of measurements of a quality characteristic in samples taken from the process versus time (or the sample number). The chart has a centre line (CL) and upper and lower control limits. The centre line represents where this process characteristic is to fall if there are no unusual sources of variability present. The control limits are determined from some simple statistical considerations.

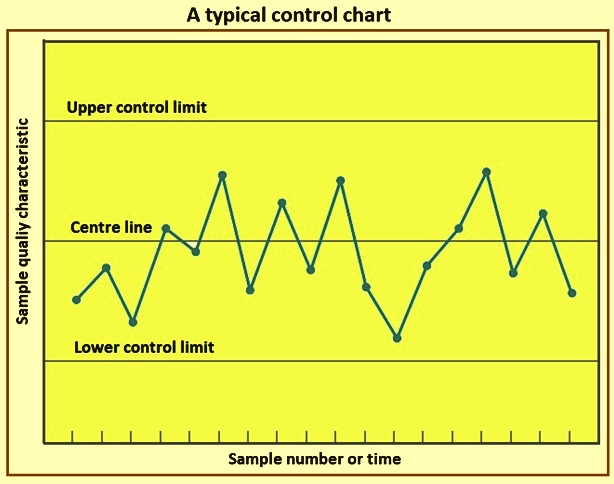
Fig 3 A typical control chart

The control limits are chosen so that if the process is in control, nearly all of the sample points fall between them. As long as the points plot within the control limits, the process is assumed to be in control, and no action is necessary. However, a point which plots outside of the control limits is interpreted as evidence that the process is out of control, and investigation and corrective action are needed to find and eliminate the assignable cause or causes responsible for this behaviour. It is customary to connect the sample points on the control chart with straight-line segments, so that it is easier to visualize how the sequence of points has evolved over time.

Even if all the points plot inside the control limits, if they behave in a systematic or non-random manner, then this can be an indication that the process is out of control. For example, if 22 of the last 25 points plotted above the centre line but below the upper control limit and only three of these points plotted below the centre line but above the lower control limit, then it is very suspicious that something is wrong. If the process is in control, all the plotted points are to have an essentially random pattern. Methods for looking for sequences or non-random patterns can be applied to control charts as an aid in detecting out-of-control conditions. Normally, there is a reason why a particular non-random pattern appears on a control chart, and if it can be found and eliminated, process performance can be improved.

The control chart is a device for describing in a precise manner exactly what is meant by statistical control. Hence, it can be used in a variety of ways. In many applications, it is used for on-line process surveillance. That is, sample data are collected and used to construct the control chart, and if the sample values of (say) fall within the control limits and do not show any systematic pattern then it can be said that the process is in control at the level indicated by the chart. It is to be noted that the interest here is in determining both whether the past data came from a process which was in control and whether future samples from this process indicate statistical control.

The most important use of a control chart is to improve the process. It has been found that, normally (i) the majority of the processes do not operate in a state of statistical control, and (ii) as a result the routine and attentive use of control charts is to identify assignable causes. If these causes can be eliminated from the process, variability can be reduced and the process can be improved. It is to be noted that the control chart only detect assignable causes and management, operator, and engineering action are normally necessary to eliminate the assignable causes.

Control charts can be classified into two general types. If the quality characteristic can be measured and expressed as a number on some continuous scale of measurement, it is normally called a variable. In such cases, it is convenient to describe the quality characteristic with a measure of central tendency and a measure of variability. Control charts for central tendency and variability are collectively called ‘variables control charts’. The chart is the most widely used chart for controlling central tendency, whereas charts based on either the sample range or the sample standard deviation are used to control process variability.

Many quality characteristics are not measured on a continuous scale or even a quantitative scale. In these cases, the judgement for each unit of product is made as either conforming or nonconforming on the basis of whether or not it possesses certain attributes, or the number of non-conformities (defects) appearing on a unit of the product can be counted. Control charts for such quality characteristics are called ‘attributes control charts’.

An important factor in control chart use is the design of the control chart. The design means the selection of the sample size, control limits, and frequency of sampling. For example, it can be specified a sample size of five measurements, three-sigma control limits, and the sampling frequency to be every hour. In most quality control problems, it is customary to design the control chart using primarily statistical considerations. The use of statistical criteria along with industrial experience has led to general guidelines and procedures for designing control charts. These procedures normally consider cost factors only in an implicit manner. Recently, however, control chart design have begun to be examined from an economic point of view, considering explicitly the cost of sampling, losses from allowing defective product to be produced, and the costs of investigating out-of-control signals which are really false alarms.

Another important consideration in control chart usage is the type of variability. When the process data vary around a fixed mean in a stable or predictable manner, the process behaviour is known as ‘stationary behaviour’. This is the type of behaviour which Shewhart implied, was produced by an in-control process. When the data are uncorrelated, that is, the observations give the appearance of having been drawn at random from a stable population, perhaps a normal distribution, and then the data is referred to by time series analysts as ‘white noise’. Time-series analysis is a field of statistics devoted exclusively to study and modelling time-oriented data. In this type of process, the order in which the data occur does not tell much that is useful to analyze the process. In other words, the past values of the data are of no help in predicting any of the future values.

There can be stationary but auto-correlated process data. These data are dependent, that is, a value above the mean tends to be followed by another value above the mean, whereas a value below the mean is normally followed by another such value. This produces a data series which has a tendency to move in moderately long ‘runs’ on either side of the mean.

There can be non-stationary variation. This type of process data occurs frequently in the process industries. In this case, the process is very unstable in that it drifts or ‘wanders about’ without any sense of a stable or fixed mean. In several industrial settings, this type of behaviour is stabilized by using engineering process control, (such as feedback control). This approach to process control is needed when there are factors which affect the process that cannot be stabilized, such as environmental variables or properties of raw materials.

Specifying of the control limits is one of the critical decisions which are to be made in designing a control chart. By moving the control limits farther from the centre line, the risk of a error is decreased, that is, the risk of a point falling beyond the control limits, indicating an out-of-control condition when no assignable cause is present. However, widening the control limits also increase the risk of an error, that is, the risk of a point falling between the control limits when the process is really out of control. If we move the control limits closer to the centre line, the opposite effect is achieved. The use of three-sigma control limits is normally justified on the basis that they give good results in practice.

Some analysts suggest using two sets of limits on control charts. The outer limits, say, at three-sigma, are the usual action limits, that is, when a point plots outside of this limit, a search for an assignable cause is made and corrective action is taken if necessary. The inner limits, usually at two-sigma, are called warning limits. If one or more points fall between the warning limits and the control limits, or very close to the warning limit, then there is suspicion that the process is not operating properly. One possible action to take when this occurs is to increase the sampling frequency and / or the sample size so that more information about the process can be obtained quickly.

The use of warning limits can increase the sensitivity of the control chart; that is, it can allow the control chart to signal a shift in the process more quickly. One of their disadvantages is that they can be confusing to operating personnel. This is not normally a serious objection, however, and many practitioners use warning limits routinely on control charts. A more serious objection is that although the use of warning limits can improve the sensitivity of the chart, they can also result in an increased risk of false alarms.

In designing a control chart, it is necessary to specify both the sample size and the frequency of sampling. In general, larger samples make it easier to detect small shifts in the process. When choosing the sample size, the size of the shift which is being tried to detect is to be kept in mind. If the process shift is relatively large, then smaller sample sizes are used than those which are to be employed if the shift of interest is relatively small. Also, the frequency of sampling is to be determined. The most desirable situation from the point of view of detecting shifts is to take large samples very frequently; however, this is normally not economically feasible. The general problem is one of allocating sampling effort. That is, either small sample is taken at short intervals or larger samples taken at longer intervals. Present industry practice tends to favour smaller, more frequent samples, particularly in high-volume manufacturing processes, or where a great many types of assignable causes can occur.

Another way to evaluate the decisions regarding sample size and sampling frequency is through the ‘average run length’ (ARL) of the control chart. Essentially, the ARL is the average number of points which is to be plotted before a point indicates an out-of-control condition. The use of ARLs to describe the performance of control charts has been subjected to criticism in recent years. The reasons for this arise since the distribution of run length for a Shewhart control chart is a geometric distribution. As a result, there are two concerns with ARL namely (i) the standard deviation of the run length is very large, and (ii) the geometric distribution is very skewed, so the mean of the distribution (the ARL) is not necessarily a very typical value of the run length. It is also occasionally convenient to express the performance of the control chart in terms of its average time to signal (ATS). If samples are taken at fixed intervals of time which are ‘h’ hours apart, then ATS = ARL x h.

Patterns on control charts are to be assessed. A control chart can indicate an out-of-control condition when one or more points fall beyond the control limits or when the plotted points show some non-random pattern of behaviour. In general, a run is a sequence of observations of the same type. In addition to runs up and runs down, the types of observations can be defined as those above and below the centre line, respectively, so that two points in a row above the centre line have a run of length 2. A run of length 8 or more points has a very low probability of occurrence in a random sample of points. As a result, any type of run of length 8 or more is frequently taken as a signal of an out-of-control condition. For example, eight consecutive points on one side of the centre line can indicate that the process is out of control.

Although runs are an important measure of non-random behaviour on a control chart, other types of patterns can also indicate an out-of-control condition. For example, the plotted sample averages can show a cyclic behaviour, yet they all fall within the control limits. Such a pattern can indicate a problem with the process such as operator fatigue, raw material deliveries, heat or stress build-up, and so forth. Although the process is not really out of control, the yield can be improved by elimination or reduction of the sources of variability causing this cyclic behaviour.

The problem is one of pattern recognition, which is, recognizing systematic or non-random patterns on the control chart and identifying the reason for this behaviour. The ability to interpret a particular pattern in terms of assignable causes needs experience and knowledge of the process. That is, not only the statistical principles of control charts are to be known, but a good understanding of the process is also necessary.

The process is normally out of control if either (i) one point plots outside the three-sigma control limits, (ii) two out of three consecutive points plot beyond the two-sigma warning limits, (iii) four out of five consecutive points plot at a distance of one-sigma or beyond from the centre line, or (iv) eight consecutive points plot on one side of the centre line. These rules apply to one side of the centre line at a time. Hence, a point above the upper warning limit followed immediately by a point below the lower warning limit does not signal an out-of-control alarm. These are frequently used in practice for enhancing the sensitivity of control charts. That is, the use of these rules can allow smaller process shifts to be detected more quickly than the case where only criterion is the normal three-sigma control limit violation.

Several criteria can be applied simultaneously to a control chart to determine whether the process is out of control. The basic criterion is one or more points outside of the control limits. The supplementary criteria are sometimes used to increase the sensitivity of the control charts to a small process shift so that people can respond more quickly to the assignable cause. Some of the sensitizing rules for control charts which are widely used in practice are (i) one or more points outside of the control limits, (ii) two of three consecutive points outside the two-sigma warning limits but still inside the control limits, (iii) four of five consecutive points beyond the one-sigma limits, (iv) a run of eight consecutive points on one side of the centre line, (v) six points in a row steadily increasing or decreasing, (vi) fifteen points in a row zone close to centre line (both above and below the centre line), (vii) fourteen points in a row alternating up and down, (viii) eight points in a row on both sides of the centre line with none in zone close to centre line, (ix) an unusual or non-random pattern in the data, and (x) one or more points near a warning or control limit.

When several of these sensitizing rules are applied simultaneously, a graduated response to out-of-control signals is frequently used. In general, care is to be exercised when using several decision rules simultaneously.

Control charts are one of the most commonly used tools. They can be used to measure any characteristics of a product. These characteristics can be divided into two groups namely variables and attributes. A control chart is used for monitoring a variable which can be measured and has a continuum of values. On the other hand, a control chart for attributes is used to monitor characteristics which have discreet values and can be counted. Frequently attributes are evaluated with a simple yes or no decision.

Control chart gives signal before the process starts deteriorating. It aids the process to perform consistently and predictably. It gives a good indication of whether problems are due to operation faults or system faults. Typical control chats are given in Fig 4.

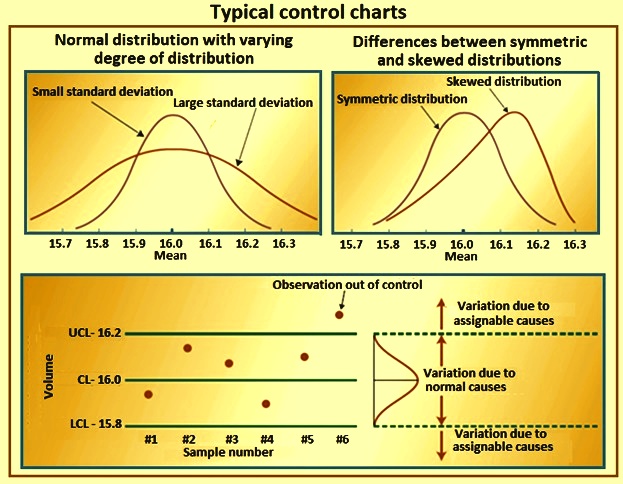
Fig 4 Typical control charts

Various types of control charts are (i) mean or x-bar chart which is the control chart used to monitor changes in the mean value or shift in the central tendency of a process (ii) range chart which is the control chart used to monitor the changes in the dispersion or variability of the process, and (iii) c-chart which is used to monitor the number of defects per unit and which is used when one can compute only the number of defects but cannot compute the proportion which is defective, and (iv) p-chart which is a control chart used to measure the proportion which is defective in a sample. The centre line in the p-chart is computed as the average proportion defective in the population p. A p-chart is used when both the total size and the number of defects can be computed. Various advantages of using the control charts are given below.

Control charts are a proven technique for improving productivity. A successful control chart program reduces scrap and rework, which are the primary productivity killers in any If the scrap and rework is reduced then productivity increases, cost decreases, and production capacity increases.
Control charts are effective in defect prevention. The control chart helps keep the process in control, which is consistent with the ‘do it right the first time’ concept. It is never cheaper to sort out ‘good’ products from ‘bad’ products later on than it is to build it right initially. If people do not have effective process control, they are paying someone to make a non-conforming product.
Control charts prevent unnecessary process adjustment. A control chart can distinguish between background noise and abnormal variation. No other device including a human operator is as effective in making this distinction. If process operators adjust the process based on periodic tests unrelated to a control chart program, they frequently overreact to the background noise and make unneeded adjustments. Such unnecessary adjustments can actually result in a deterioration of process performance. In other words, the control chart is consistent with the ‘if it is not broken, do not fix it’ concept.
Control charts provide diagnostic information. Frequently, the pattern of points on the control chart contains information of diagnostic value to an experienced operator or engineer. This information allows the implementation of a change in the process which improves its performance.
Control charts provide information about process capability. It provides information about the value of important process parameters and their stability over time. This allows an estimate of process capability to be made. This information is of tremendous use to product and process designers.

Control charts are among the most important management control techniques. They are as important as cost controls and material controls. Modern computer technology has made it easy to implement control charts in any type of process, as data collection and analysis can be performed on a micro-computer or a local area network terminal in real-time, on-line at the work centre.

Cause and effect analysis diagram

When people are able to relate different causes to the effect, namely the quality characteristics, then they can use this logical thinking of cause and effect for further investigations to improve and control the quality. This type of linking is done through cause and effect diagrams.

Cause and effect analysis was devised by Professor Kaoru Ishikawa, a pioneer of quality management, in 1968. Cause and effect analysis diagram is also known as Ishikawa diagram, Herringbone diagram, or Fishbone diagram (since a completed diagram can look like the skeleton of a fish). Cause and effect analysis diagram technique combines brain-storming with a type of mind map. It pushes people to consider all possible causes of a problem, rather than just the ones which are most obvious.

Cause and effect analysis diagrams are casual diagrams which show the causes of a specific event. Common uses of these diagrams are (i) product design and quality defect prevention, and (ii) to identify potential factors causing an overall effect. Each cause or reason for imperfection is a source of variation.

Causes are normally grouped into six major categories to identify these sources of variation. These six categories are (i) people which include the person involved with the process, (ii) methods which include how the process is performed and the specific requirements for doing it, such as policies, procedures, rules, regulations and laws etc., (iii) machines under which comes equipment, computers and tools etc. which are needed to carry out the job, (iv) materials which include raw materials, consumables, spare parts, pens and paper, etc. used to produce the final product, (v) measurements which are the data generated from the process that are used to evaluate its quality, and (vi) environment which is the conditions, such as location, time, temperature, and culture in which the process operates. A cause and effect analysis diagram is shown in Fig 5.

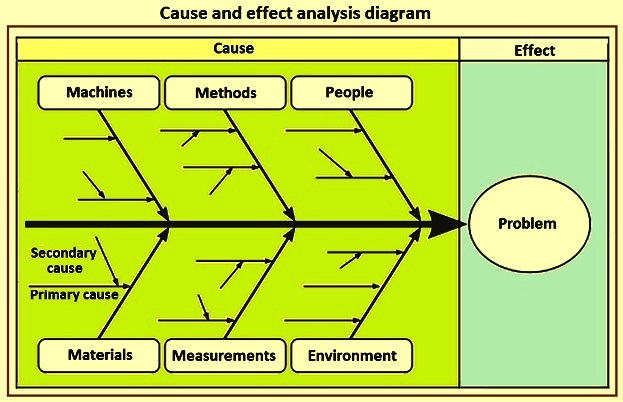
Fig 5 Cause and effect analysis diagram

Cause and effect analysis diagram is an extremely powerful technique. A highly detailed cause and effect analysis diagram can serve as an effective troubleshooting aid. In addition, the construction of a cause and effect analysis diagram, as a team experience, tends to get people involved in attacking a problem rather than in affixing blame.

Stratification

Stratification is a technique used in combination with other data analysis techniques. When data from a variety of sources or categories have been lumped together, the meaning of the data can be impossible to see. The technique separates the data so that the pattern can be seen. Stratification can be used in the cases (i) before collecting the data (ii) when data come from several sources or conditions such as shifts, days of week, suppliers, materials, products, departments, equipment, or population groups, and (iii) when data analysis can need separating different sources or conditions. Stratification procedure consists of the following three steps.

Before collecting data, one has to consider which information about the sources of the data can have effect on the results. During data collection, data related to this information are to be collected as well.
When plotting or graphing the collected data on a scatter diagram, control chart, histogram or other analysis technique, different marks or colours need to be used to distinguish from data from various sources. Data which are distinguished in this way are said to be ‘stratified’.
The subsets of stratified data are analyzed separately.

An example of data stratification is given in Fig 6 on a scatter diagram.

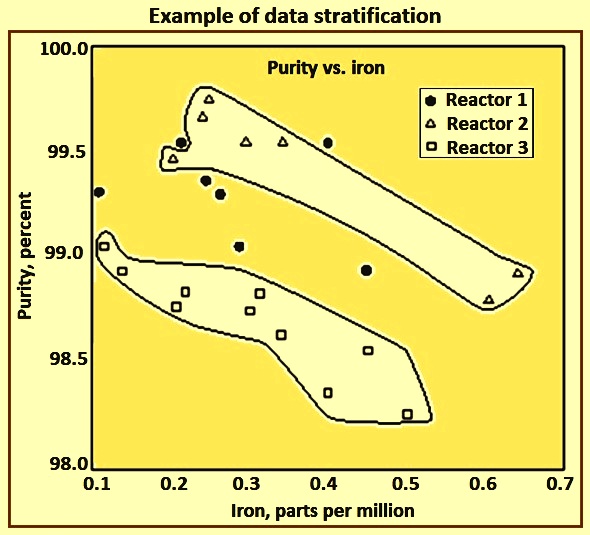
Fig 6 Example of data stratification

Scatter diagram

The scatter diagram consists of graphs drawn with pairs of numerical data, with one variable on each axis, to look or relationship between them. If the variables are correlated, the points fall along a line or curve. A scatter diagram is a type of mathematical diagram using Cartesian coordinates to display values for two variables for a set of data. The data is displayed as a collection of points, each having the value of one variable determining the position on the horizontal axis (x axis) and the value of the other variable determining the position on the vertical axis (y axis).

A scatter diagram is used when a variable exists which is below the control of the operator. If a parameter exists which is systematically incremented and / or decremented by the other, it is called the control parameter or independent variable and is customarily plotted along the x axis. The measured or dependent variable is customarily plotted along the y axis. If no dependent variable exists, either type of variable can be plotted on either axis or a scatter diagram illustrates only the degree of correlation (not causation) between two variables.

The scatter diagram is a useful plot for identifying a potential relationship between two variables. Data are collected in pairs on the two variables, say, (yi, xi) – for i = 1, 2, . . . ., and n. Then yi is plotted against the corresponding xi. The shape of the scatter diagram frequently indicates what type of relationship can exist between the two variables. Scatter diagrams are very useful in regression modelling. Regression is a very useful technique in the analyze step of DMAIC. Typical scatter diagrams are shown in Fig 7.

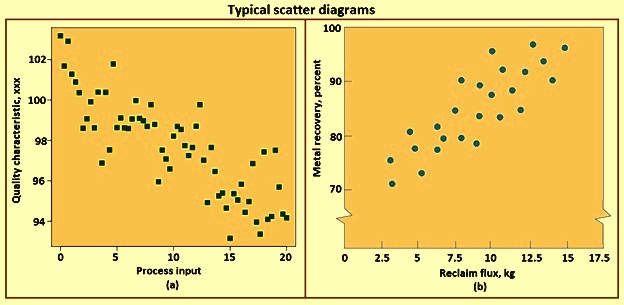
Fig 7 Typical scatter diagrams

Fig 7b shows a scatter diagram relating metal recovery (in percent) from a magna-thermic smelting process for magnesium against corresponding values of the amount of reclaim flux added to the crucible. The scatter diagram indicates a strong positive correlation between metal recovery and flux amount, that is, as the amount of flux added is increased, the metal recovery also increases. It is tempting to conclude that the relationship is one based on cause and effect. By increasing the amount of reclaim flux used, one can always ensure high metal recovery. This thinking is potentially dangerous, since correlation does not necessarily imply causality.

This apparent relationship can be caused by something quite different. For example, both variables can be related to a third one, such as the temperature of the metal prior to the reclaim pouring operation, and this relationship can be responsible for what is seen in Fig 7. If higher temperatures lead to higher metal recovery and the practice is to add reclaim flux in proportion to temperature, then the addition of more flux when the process is running at low temperature does nothing to enhance yield. The scatter diagram is useful for identifying potential relationships. Designed experiments are to be used to verify causality.

Benefits of SQC

During the 100 % inspection, unwanted variations in quality can be detected after large number of defective items has already been produced whereas in SQC technique the moment a sample point falls outside the control limits, it is taken as a danger signal and necessary corrective measures are taken. There are several benefits of SQC over 100 % inspections.

The benefits of SQC include (i) it needs lesser time as compared to the 100 % inspection and hence the efficiency increases, (ii) it provides a means of detecting error at inspection, (iii) it leads to more uniform quality of production, (iv) it improves the relationship with the customer, (v) it reduces inspection costs since only a fractional output is inspected, (vi) it reduces the number of rejections and saves the cost of material, (vii) it provides a basis for attainable specifications, (vi) it points out the bottlenecks and trouble spots, (vii) it provides a means of determining the capability of the manufacturing process, (viii) specification can easily be predicted for the future, which is not possible even with 100 % inspection, (ix) in cases where destruction of product is necessary for inspecting it, 100 % inspection is not possible (since it spoils all the products), sampling inspection is resorted to, (x) it promotes the understanding and appreciation of quality control, and (xi) once the SQC plan is established, it is easy to apply even by man who does not have extensive specialized training.